이 글은 누구나 자료 구조와 알고리즘(저자 : 제이 웬그로우)의 내용을 개인적으로 정리하는 글임을 알립니다.

버블 정렬

버블 정렬은 단순 정렬(simple sort)이라 알려졌다.

이해하기 쉬워서 이렇게 불리지만, 더 빠르다고 알려진 정렬 알고리즘보다 비효율적이다.

버블 정렬은 아래와 같은 단계를 따른다.

1. 배열 내에서 연속된 두 항목을 가리킨다. 즉, 첫 번째 항목과 두번째 항목을 비교한다.

2. 두 항목의 순서가 뒤바뀌어있으면, 두 항목을 교환한다. (순서가 올바르다면 2단계에선 아무것도 하지 않는다.)

3. 포인터를 오른쪽으로 한 셀씩 옮긴다.

4. 배열의 끝까지 또는 이미 정렬된 값까지 1단계부터 3단계를 반복한다.
이제 배열의 첫 패스스루(pass-through)가 끝났다. 즉, 배열 끝까지 값을 하나하나 가리키며 배열을 통과했다.

5. 이제 두 포인터를 다시 배열의 처음 두 값으로 옮겨서 1단계부터 4단계를 다시 실행함으로써 새로운 패스스루를 실행한다.
교환이 일어나지 않는 패스스루가 생길 때까지 패스스루를 반복한다.
교환할 항목이 없다는 것은 배열이 정렬됐고 문제를 해결했다는 뜻이다.

더 자세히 버블 정렬 살펴보기

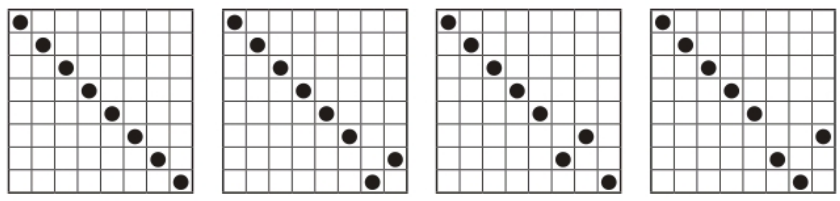
[4, 2, 7, 1, 3] 이라는 배열을 정렬하고 싶다고 가정하자.

순서가 뒤죽박죽인 데다 중복 값까지 있는 배열을 올바르게 오름차순으로 정렬해야한다.

첫 번째 패스스루 시작

배열의 처음 상태는 아래와 같다.

1단계 : 먼저 4와 2를 비교한다.

2단계 : 순서가 맞지 않으므로 둘을 교환한다.

3단계 : 다음으로 4와 7을 비교한다.

순서가 올바르기 때문에 교환할 필요가 없다.

4단계 : 7과 1을 비교한다.

5단계 : 순서가 맞지 않으므로 교환한다.

6단계 : 7과 3을 비교한다.

7단계 : 순서가 맞지 않으므로 교환한다.

이제 7은 확실히 배열 내에서 올바른 위치에 있다.

적절한 위치에 도달할 때까지 7을 계속해서 오른쪽으로 옮겼기 때문이다.

이 알고리즘을 버블 정렬이라 부르는 까닭이 여기에 있다.

각 패스스루마다 정렬되지 않은 값중 가장 큰 값, 버블이 올바른 위치로 가게 된다.

첫 번째 패스스루에서 교환을 적어도 한 번 수행했으니 다음 패스스루도 수행해야 한다.

두 번째 패스스루 시작

8단계 : 2와 4를 비교한다.

올바른 순서이므로 다음 단계로 넘어간다.

9단계 : 4와 1을 비교한다.

10단계 : 순서가 맞지 않으므로 교환한다.

11단계 : 4와 3을 비교한다.

12단계 : 순서가 맞지 않으므로 교환한다.

첫 번째 패스스루를 통해 7이 이미 올바른 위치라는 것을 알고 있으니 4와 7은 비교할 필요가 없다.

또한, 이제 4 역시 올바른 위치로 올라갔다.

이로써 두 번째 패스스루도 끝났다.

두 번째 패스스루에서 교환을 적어도 한 번 수행했으니 다음 패스스루를 수행해야 한다.

세번째 패스스루 시작

13단계 : 2와 1을 비교한다.

14단계 : 순서가 맞지 않으니 교환한다.

15단계 : 2와 3을 교환한다.

순서가 올바르니 교환할 필요가 없다.

이제 3이 올바른 위치로 갔다.

세 번째 패스스루에서 교환을 적어도 한 번 수행했으니 다음 패스스루를 수행해야 한다.

네 번째 패스스루 시작

16단계 : 1과 2를 비교한다.

순서가 올바르니 교환할 필요가 없다. 나머지 값은 모두 이미 정렬되었으니 네 번째 패스스루를 종료할 수 있다.

어떤 교환도 하지 않은 패스스루였으므로 이제 이 배열은 완전히 정렬되었다.

버블 정렬 구현

아래의 코드는 버블 정렬을 파이썬으로 구현한 코드이다.

def bubble_sort(list):
    unsorted_until_index = len(list) - 1
    sorted = False

    while not sorted:
        sorted = True
        for i in range(unsorted_until_index):
            if list[i] > list[i+1]:
                list[i], list[i+1] = list[i+1], list[i]
                sorted = False
        unsorted_until_index -= 1

    return list

버블 정렬의 효율성

버블 정렬 알고리즘은 두 가지 중요한 단계를 포함한다.

• 비교 : 어느쪽이 더 큰지 두수를 비교한다.
• 교환 : 정렬하기 위해 두 수를 교환한다.

먼저 버블 정렬에서 얼마나 많은 비교가 일어났는지 보면

5개의 원소를 갖는 배열에서

첫 번째 패스스루 : 4번

두 번째 패스스루 : 3번

세 번째 패스스루 : 2번

네 번째 패스스루 : 1번

총 : 4 + 3 + 2 + 1 = 10번의 비교가 일어났다.

즉, 원소가 N개 있을 때, (N-1) + (N-2) + (N-3) + ... + 1번의 비교를 수행한다.

버블 정렬에서 얼마나 교환이 일어났는지 보면

배열이 오름차순이 아닌 내림차순으로 정렬되어 있는 최악의 시나리오라면 비교할때마다 교환을 해야한다.

이런 시나리오에서는 비교 10번, 교환 10번이 일어나 총 20단계가 필요하다.

값 10개가 역순으로 된 배열에서는 45번의 비교와 45번의 교환이 일어나 총 90단계이고,

값 20개가 역순으로 된 배열에서는 190번의 비교와 190번의 교환이 일어나므로 총 380단계이다.

원소가 N개일 때, 단계는 대략 N²인 것을 확인할 수 있다.

따라서 버블 정렬의 시간 복잡도를 빅 오 표기법으로 나타내면 원소가 N개일때, N²단계가 필요하므로 O(N²)이다.

O(N²)은 데이터가 증가할 때 단계 수가 급격히 늘어나므로 비교적 비효율적인 알고리즘으로 간주된다.

참고로 O(N²)을 이차 시간이라고도 부른다.

또한 중첩 반복문을 사용하는 알고리즘은 대부분 O(N²)의 시간복잡도를 가진다.

문제설명

소스코드

import java.util.Scanner;

class Main {
	static boolean[] flag_a = null;
    static boolean[] flag_b = null;
    static boolean[] flag_c = null;
    static int[] pos = null;
	static void func(int N)
	{
		flag_a = new boolean[N];
	    flag_b = new boolean[2 * N + 1];
	    flag_c = new boolean[2 * N + 1];
	    pos = new int[N];
	}
    static int count = 0;
    static void set(int i, int N) 
    {
        for (int j = 0; j < N; j++) 
        {
            if (flag_a[j] == false && flag_b[i + j] == false && flag_c[i - j + N - 1] == false)
            {        
                pos[i] = j;
                if (i == N-1) ++count;
                else 
                {
                    flag_a[j] = flag_b[i + j] = flag_c[i - j + (N - 1)] = true;
                    set(i + 1, N);
                    flag_a[j] = flag_b[i + j] = flag_c[i - j + (N - 1)] = false;
                }
            }
        }
    }
    public static void main(String[] args) {
    	Scanner sc = new Scanner(System.in);
    	int N = sc.nextInt();
    	func(N);
        set(0, N);
        System.out.print(count);
    }
}

설명

2023.08.29 - [자료구조 & 알고리즘/알고리즘] - [Java] 8퀸 문제(분기한정법)

Do it! 자료구조와 함께 배우는 알고리즘 입문[자바편] 연습문제와 실습문제입니다.

8퀸 문제란?

• 서로 공격하여 잡을 수 없도록 8개의 퀸을 8x8 체스판에 놓는 것

퀸은 현재 놓여있는 지점에서 가로 or 세로 or 대각선의 8가지 방향으로 직선 이동 가능하다.

체스판의 가로줄을 행, 세로줄을 열이라 하고 배열 인덱스에 맞추어 행과 열에 0~7의 번호를 부여한다.

이 문제의 답이 되는 조합은 92가지이다.

아래의 그림은 92가지중 하나의 조합을 나타낸 것이다.

퀸 배치하기

8개의 퀸을 체스판 64칸(8*8)이므로 처음에 64칸중 아무칸에 놓고, 다음 퀸을 배치할 때는 나머지 63칸에서 임의로 선택한다.

• 64 x 63 x 62 x 61 x 60 x 59 x 58 x 57 = 178,462,987,637,760

이 조합을 모두 나열하고 각각의 조합이 8퀸 문제의 조건을 만족하는지 조사하는 것은 현실적이지 않다.

따라서 규칙 하나를 세운다.

• 규칙1 : 각 열에 퀸을 1개만 배치한다.

이러면 퀸을 배치하는 조합의 수는 16,777,216가지로 많이 줄어들지만 아직도 여전히 많다.

그렇기에 규칙 하나를 더 추가한다.

• 규칙2 : 각 행에 퀸을 1개만 배치한다.

아래의 그림은 규칙1과 규칙2를 모두 만족하는 배치의 일부(4가지)를 나타낸 것이다.

이렇게 하면 이 조합을 나열하는 알고리즘을 어떻게든 만들 수 있다.

하지만 그렇게 간단히 만들어 지지는 않는다.

이제 문제를 정리하기 위해 처음으로 다시 돌아가 규칙 1에 따라 조합을 나열하는 알고리즘을 생각하면

모든 열에 퀸이 아직 배치되지 않은 상태이다.

첫 번째 열에 퀸을 배치하는 경우의 수는 8개이다.

두 번째 열에 퀸을 배치하는 경우의 수 또한 8개이다.

여기서 규칙2를 적용해서 같은 행에 여러 퀸을 배치하는 조합은 없애버리자.

분기 조작(규칙 1)

분기란 가지가 뻗어 나가듯이 문제를 나누어 푸는 과정을 의미
또한 지금은 모든 조합만 나열하고, 8퀸 문제 해결은 마지막에 다룬다.

배열 pos는 퀸의 배치를 나타낸다.

i열에 놓인 퀸의 위치가 j행이면 pos[i]의 값을 j로 한다.

즉, pos[1]의 값이 4이면 1열의 퀸이 4행에 배치된 상태를 의미한다.

set 메소드는 pos[i]에 0부터 7까지의 값을 순서대로 대입하여 i열에 퀸을 1개만 배치하는 8가지 조합을 만드는 재귀 메소드이다.

매개변수 i가 이 퀸을 배치할 열이다.

class QueenB {
    static int[] pos = new int[8];    // 각 열의 퀸의 위치

    //--- 각 열의 퀸의 위치를 출력 ---//
    static void print() {
        for (int i = 0; i < 8; i++)
            System.out.printf("%2d", pos[i]);
        System.out.println();
    }

    //--- i열에 퀸을 배치 ---//
    static void set(int i) {
        for (int j = 0; j < 8; j++) {
            pos[i] = j;            // 퀸을 j행에 배치함
            if (i == 7)            // 모든 열에 배치함
                print();
            else
                set(i + 1);        // 다음 열에 퀸을 배치
        }
    }

    public static void main(String[] args) {
        set(0);                   // 0 열에 퀸을 배치
    }
}

이렇게 하면 규칙1을 적용한 것과 같이 16,777,216가지의 조합이 모두 나열된다.

이런 방법을 분기 조작 또는 가지 뻗기라고 한다.

분기 한정법(규칙 1 + 규칙 2)

class Main{
    static boolean[] flag = new boolean[8];        // 각 행에 퀸이 이미 배치되었는가?
    static int[] pos = new int[8];                 // 각 열의 퀸의 위치

    //--- 각 열의 퀸의 위치를 출력 ---//
    static void print() {
        for (int i = 0; i < 8; i++)
            System.out.printf("%2d", pos[i]);
        System.out.println();
    }

    //--- i열의 알맞은 위치에 퀸을 배치 ---//
    static void set(int i) {
        for (int j = 0; j < 8; j++) {
            if (flag[j] == false) {    // j 행에 퀸을 아직 배치하지 않음
                pos[i] = j;            // 퀸을 j행에 배치함
                if (i == 7)            // 모든 열에 배치함
                    print();
                else {
                    flag[j] = true;
                    set(i + 1);
                    flag[j] = false;
                }
            }
        }
    }

    public static void main(String[] args) {
        set(0);
    }
}

위 알고리즘에서는 flag라는 배열을 사용한다.

flag는 같은 행에 중복하여 퀸이 배치되는 것을 방지하기 위한 표시이다.

 j행에 퀸을 배치하면 flag[j]의 값을 true로 하고, 배치되지 않은 상탯값은 false로 설정한다.

set(i + 1) 메소드 실행이 끝나면 다음 경우의 수를 위해 퀸을 j행에서 제거한다(flag[j] = false)

set 메소드에서는 퀸을 아직 배치하지 않은 행에만 퀸을 배치한다.

이렇게 필요하지 않은 분기를 없애 불필요한 조합을 줄이는 방법을 한정 조작이라 하고, 분기 조작과 한정 조작을 조합하여 문제를 풀어가는 방법을 분기 한정법이라고 한다.

아직까지는 퀸이 행 방향과 열 방향으로 겹쳐지지 않는 조합을 나열하기만 한 것이다.

퀸은 대각선 방향으로도 이동할 수 있기 때문에 어떤 대각선에서 보더라도 퀸을 1개만 배치하는 한정 조작을 추가해야 한다.

8퀸 문제 해결 코드

class Main {
    static boolean[] flag_a = new boolean[8];     // 각 행에 퀸이 이미 배치되었는가?
    static boolean[] flag_b = new boolean[15];    // 대각선 ↙에 퀸이 이미 배치되었는가?
    static boolean[] flag_c = new boolean[15];    // 대각선 ↘에 퀸이 이미 배치되었는가?
    static int[] pos = new int[8];    // 각 열의 퀸의 위치

    //--- 각 열의 퀸의 위치를 출력 ---//
    static void print() {
        for (int i = 0; i < 8; i++)
            System.out.printf("%2d", pos[i]);
        System.out.println();
    }

    //--- i열의 알맞은 위치에 퀸을 배치 ---//
    static void set(int i) {
        for (int j = 0; j < 8; j++) 
        {
            if (flag_a[j] == false &&                // 가로(j행)에 아직 배치하지 않음
                flag_b[i + j] == false &&            // 대각선 ↙에 아직 배치하지 않음
                flag_c[i - j + 7] == false) 		 // 대각선 ↘에 아직 배치하지 않음
            {        
                pos[i] = j;                              // 퀸을 j행에 배치함
                if (i == 7) print();
                else 
                {
                    flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true;
                    set(i + 1);
                    flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false;
                }
            }
        }
    }

    public static void main(String[] args) {
        set(0);
    }
}

• flag_b와 flag_c는 / 방향과 \방향의 대각선 위에 퀸을 배치했는지 체크하는 배열이다.

print 메소드를 수정하여 아래의 그림과 같이 퀸의 배치 상황을 출력하는 메소드를 작성

class Main {

	static boolean[] flag_a = new boolean[8];		// 각행에 퀸을 배치했는지 체크
	static boolean[] flag_b = new boolean[15];		// /대각선에 퀸을 배치했는지 체크
	static boolean[] flag_c = new boolean[15];		// ＼대각선에 퀸을 배치했는지 체크
	static int[] pos = new int[8];	// 각열의 퀸의 위치

	//--- 배치 상황(각열의 퀸의 위치)을 출력 ---//
	static void print() {
		for (int i = 0; i < 8; i++) {
			for (int j = 0; j < 8; j++)
					System.out.printf("%s", j == pos[i] ? "■" : "□");
			System.out.println();
		}
		System.out.println();
	}

	//--- i열의 알맞은 위치에 퀸을 배치 ---//
	static void set(int i) {
		for (int j = 0; j < 8; j++) {
			if (flag_a[j] == false &&						// 가로(j행)에 미배치
					flag_b[i + j] == false &&				// /대각선에 미배치
					flag_c[i - j + 7] == false) {		// ＼대각선에 미배치
				pos[i] = j;					// 퀸을 j행에 배치
				if (i == 7)					// 모든 열에 배치 마침
					print();
				else {
					flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true;
					set(i + 1);
					flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false;
				}
			}
		}
	}

	public static void main(String[] args) {
		set(0);
	}
}​

8퀸 문제를 비재귀적으로 구현

class Main {

	static boolean[] flag_a = new boolean[8];		// 각행에 퀸을 배치했는지 체크
	static boolean[] flag_b = new boolean[15];		// /대각선에 퀸을 배치했는지 체크
	static boolean[] flag_c = new boolean[15];		// ＼대각선에 퀸을 배치했는지 체크
	static int[] pos = new int[8];	// 각열의 퀸의 위치

	//--- 배치 상황(각열의 퀸의 위치)을 출력 ---//
	static void print() {
		for (int i = 0; i < 8; i++) {
			for (int j = 0; j < 8; j++)
				System.out.printf("%s", j == pos[i] ? "■" : "□");
			System.out.println();
		}
		System.out.println();
	}

	//--- i열의 알맞은 위치에 퀸을 배치 ---//
	static void set(int i) {
		int j;
		int[] jstk = new int[8];

		Start : while (true) {
			j = 0;
			while (true) {
				while (j < 8) {
					if (!flag_a[j] && !flag_b[i + j] && !flag_c[i - j + 7]) {
						pos[i] = j;
						if (i == 7)								// 모든 열에 배치종료
							print();
						else {
							flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true;
							jstk[i++] = j;					// i열의 행을 Push
							continue Start;
						}
					}
					j++;
				}
				if (--i == -1) return;
				j = jstk[i];									// i열의 행을 Pop
				flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false;
				j++;
			}
		}
	}

	public static void main(String[] args) {
		set(0);
	}
}​

Do it! 자료구조와 함께 배우는 알고리즘 입문[자바편] 연습문제와 실습문제입니다.

public class Main {
	static void recur(int n)
	{
	    if(n > 0)
	    {
	        recur(n - 1);
	        System.out.println(n);
	        recur(n-2);
	    }
	}
	
    public static void main(String[] args) throws Exception
    {
    	recur(4);
    }
}
/*
1
2
3
1
4
1
2
*/

위 recur 메소드는 실행 과정에서 같은 계산을 여러번 반복하여 수행한다.

위 에서 보는 것과 같이 recur(4)를 호출하면 recur(1)을 3회 실행한다.

n 값이 커지면 반복하는 계산 횟수는 더욱 늘어난다.

recur(3)은 1, 2, 3, 1을 차례로 출력하므로 출력할 문자열"1\n2\n3\n1"을 메모한다.

다시 recur(3)이 호출되었을 때 메모해 둔 문자열을 화면에 출력하면 중복하여 계산할 필요가 없다.

여기서 메모화 기법을 사용하면 동일한 계산을 반복하지 않고 1회만 수행할 수 있다.

import java.util.Scanner;

class RecurMemo {
    static String[] memo;

    //--- 메모화를 도입한 메서드 recur ---//
    static void recur(int n) {
        if (memo[n + 1] != null)
            System.out.print(memo[n + 1]);                              // 메모를 출력
        else {
            if (n > 0) {
                recur(n - 1);
                System.out.println(n);
                recur(n - 2);
                memo[n + 1] = memo[n] + n + "\n" + memo[n - 1];        // 메모화
            } else {
                memo[n + 1] = "";     // 메모화 : recur(0)과 recur(-1)은 빈 문자열
            }
        }
    }

    public static void main(String[] args) {
        Scanner stdIn = new Scanner(System.in);

        System.out.print("정수를 입력하세요 : ");
        int x = stdIn.nextInt();

        memo = new String[x + 2];
        recur(x);
    }
}

구체적으로 보면 memo에 메모하는 과정은 아래와 같다.

이 글은 누구나 자료 구조와 알고리즘(저자 : 제이 웬그로우)의 내용을 개인적으로 정리하는 글임을 알립니다.

빅 오

단순히 어떤 알고리즘을 22단계 알고리즘, 400단계 알고리즘이라고 표시할 수 없다.

알고리즘에 필요한 단계 수를 하나의 수로 못 박을 수 없기 때문이다.

예를 들어 선형 검색에는 배열의 원소 수만큼의 단계가 필요하므로 배열에 따라 필요한 단계 수가 다르다.

선형 검색의 효율성을 정량화하는 보다 효과적인 방법은 배열에 N개의 원소가 있을 때 선형 검색에 N단계가 필요하다고 표현한다.

빅 오 표기법을 사용해 주어진 알고리즘의 효율성을 쉽게 분류하고 이해시킬 수 있다.

• 선형 검색 알고리즘을 빅 오로 나타내면 O(N)이다.
• O(N)은 알고리즘에 N단계가 필요하다는 뜻이다.
• 원소가 N개인 배열의 읽기는 딱 한 단계가 필요하므로 O(1)이다.
• 원소가 N개인 배열의 검색에는 N개의 단계가 필요하다.

배열의 읽기는 원소가 몇개이든 간에 한 단계만 거치면 되기 때문에 O(1)로 표기하고, O(1)은 가장 빠른 알고리즘으로 분류된다.

데이터가 늘어나도 O(1) 알고리즘의 단계 수는 증가하지 않는다. 

N이 얼마든 항상 상수 단계만 필요하다. 그래서 O(1) 알고리즘을 상수 시간을 갖는 알고리즘이라고도 표현한다.

데이터가 몇 개든 항상 3단계 걸리는 알고리즘은 O(3)??

빅 오의 본질은 데이터가 늘어날 때 알고리즘의 성능이 어떻게 바뀌는지를 뜻한다.
빅 오는 단순히 알고리즘에 필요한 단계수만 알려주지 않는다.
데이터가 늘어날 때 단계 수가 어떻게 증가하는지 설명한다.

이러한 관점에서 보면 O(1)이든 O(3)이든 별로 중요하지 않다.

두 알고리즘 모두 데이터 증가에 영향을 받지 않는, 즉 단계수가 변하지 않는 유형이므로 본질적으로 같은 알고리즘 유형이다.

따라서 O(3)이든 O(6)이든 O(1000)이든 모두 O(1)로 표기한다.

빅 오의 본질 더 파고들기

데이터 크기에 상관없이 항상 100단계가 걸리는 알고리즘과 O(N)인 알고리즘이 있다고 가정하자.

• 100보다 큰 모든 배열에서는 O(N)의 알고리즘에 더 많은 단계가 걸린다.
• 즉, 0~100개의 데이터를 가진 데이터 집합보다 101~무한대까지 데이터를 가진 데이터 집합이 더 많기 때문에  O(1)알고리즘에 실제로 몇 단계가 걸리든 O(N)이 전반적으로 O(1)보다 덜 효율적이라 할 수 있다.
• 항상 백만 단계가 걸리는 O(1) 알고리즘이라도 마찬가지이다. 데이터가 증가할수록 O(N)이 O(1)보다 덜 효율적인 어떤 지점에 반드시 다다르게 되며, 이 지점부터 데이터 양이 무한대로 갈 때까지 바뀌지 않는다.

같은 알고리즘, 다른 시나리오

선형 검색이 항상 O(N)은 아니다.

선형 검색의 효율성은 최선의 시나리오에선 O(1), 최악의 시나리오에서는 O(N)이다.

별도로 명시하지 않는 한 빅 오 표기법은 일반적으로 최악의 시나리오를 의미한다.

이는 비관적인 접근이 유용한 도구일 수 있기 때문이다.

최악의 시나리오에서 알고리즘이 얼마나 비효율적인지 정확히 알면 최악을 대비함과 동시에 알고리즘의 선택에 중요한 영향을 미칠 수 있다.

O(log N)

이진 검색을 빅 오 표기법의 관점에서는 데이터가 커질수록 단계 수가 늘어나므로 이진 검색은 O(1)이라 표현할 수 없다.

또한, 검색하고 있는 원소 수보다 단계수가 훨씬 적으므로 O(N)의 부류에도 맞지 않는다.

빅 오는 이진 검색의 시간 복잡도를 O(log N)으로 표현한다. (로그의 밑은 10이 아니라 2가 생략된 것이다.)

이러한 유형의 알고리즘을 로그 시간의 시간 복잡도라고 말한다.

O(log N)은 데이터가 두 배로 증가할 때마다 한 단계식 늘어나는 알고리즘을 설명하는 빅 오의 방법이다.

O(1), O(N), O(log N)을 그래프로 비교하면 아래와 같다.

로가리즘
로그는 로가리즘(logarithm)의 줄임말이다.
로가리즘은 지수와 역의 관계다.

2^3 은 2 x 2 x 2와 동치로서 값이 8이다.
log₂8은 2³의 역이다. 즉, 2를 몇 번 곱해야 8을 얻을 수 있는지를 뜻한다.
2를 세 번 곱해야 8이 나오므로 log₂8 = 3이다.

log₂8을 다른 방식으로 설명하면, 1이 될 때까지 8을 2로 계속해서 나눌 때 등식에 얼마나 많은 2가 등장하는지를 나타낸다.
즉 1이 나올때 까지 8을 2로 몇 번 나눠야 하는지이다.
8 / 2 / 2 / 2 = 1, 총 3번이다.

O(log N)의 해석

O(log N)은 log₂N을 줄여 부르는 말이다.

O(log₂N)은 데이터 원소가 N개 있을 때 알고리즘에 log₂N단계가 걸린다는 의미다.

원소가 8개 있으면 log₂8 = 3이므로 3단계가 걸린다.

바꿔 말해 원소 8개를 절반으로 계속해서 나누면 원소가 하나 남을 때까지 3단계가 걸릴 것이다.

이진 검색이 정확히 이렇게 동작한다.

즉, O(logN)은 원소가 하나가 될 때까지 데이터 원소를 계속해서 반으로 줄이는 만큼의 단계수가 걸린다는 뜻이다.

변수

변수의 개념

변수 : 값을 저장할 때 사용하는 식별자

파이썬에서는 숫자형/문자형을 비롯한 모든 데이터 타입에 대해 그것을 지칭할 수 있는 이름을 자유롭게 만들 수 있고 (키워드는 변수이름으로 사용 못함), 컴퓨터 하드웨어 중 메모리에 변수에 대한 공간을 만들고, 값을 할당함

컴퓨터의 메모리 공간에 이름을 붙이는 것으로 우리는 여기에 값을 저장할 수 있다.

C언어에서는 직접 메모리 상의 공간에 접근할 수 있는‘포인터’를 제공하고 있으나, 파이썬에서는 포인터가 없고, 단지 객체의 참조값만 확인할 수 있음

불변 객체와 가변 객체

불변 객체

• 불변 객체(immutable object)은 한번 만들어지면 변경할 수 없는 객체
• 우리가 변수에 저장된 값을 변경하면 값을 저장하는 새로운 객체가 생성되어서 새로운 객체의 참조값이 변수에 저장됨
• 정수, 실수, 문자열, 튜플 등

가변 객체

• 가변 객체(mutable object)는 변경할 수 있는 객체
• 리스트, 세트, 딕셔너리 등

입력

• 프로그램을 만들다 보면, 사용자로부터 입력을 받아서 활용하는 경우가 많음
• 파이썬의 경우 사용자 입력을 받을 때 input() 함수를 사용하여 받을 수 있음
• input() 함수를 통해 입력 받은 값은 변수에 할당할 수 있음

• input() 함수를 통해 입력 받은 값의 데이터 타입은
  무조건 문자열(str) 형태
• 따라서 숫자를 넣어줬으면, 
  문자열 → 숫자형으로 변형시켜줘야 함
• 문자형 → 정수형/실수형으로 변형할 수 있는
  int(), float() 함수를 사용해야 함

문자열

• 문자와 단어 등으로 구성된 문자들의 집합을 의미
• Python의 문자열은 유니 코드 문자를 나타내는 바이트 배열
• 단일 문자는 길이가 1 인 문자열
• 숫자도 따옴표 안에 있으면 문자열
• 파이썬의 문자열 리터럴은 작은 따옴표 또는 큰 따옴표로 묶음
  -> 작은 따옴표 또는 큰 따옴표 세 개를 연달아 입력하는 방법도 가능

간단한 문자열 만들어 보기
• “Hello” • ‘안녕하세요’
• '''문자열을 공부하고 있습니다.'''
• """문자열을 공부하고 있습니다."""

문자열 내부에 따옴표를 넣으려면?

• 큰따옴표(작은따옴표) 안에 작은따옴표(큰따옴표)로 문자를 표기해야 함
• ""안에 ""을 넣는다면, 단순 문자열이 두 번 반복되는 걸로 파이썬 인터프리터는 이해함
  예 : ""안녕"하세요" → “”, “하세요” 가 독립된 문자열로 인식됨. 안녕은 문자열로 인식도 안됨
• 혹은 이스케이프 문자 (역슬래쉬 ＼ 기호와 함께 사용, 한국어 키보드에서는 원화표시 ￦)를 함께 사용
  예 : ＼', ＼''

문자열 연산

• 문자열 연산에도 숫자형과 비슷하게 +, * 연산을 적용할 수 있음
• + : 주어진 여러 문자열 연결 (합치기)
  문자열 + 문자열 + ,,, + 문자열 (O) 
  문자열 + 숫자형 (X)
•  * : 주어진 문자열 반복
  문자열 * 반복 횟수(숫자)
  반복 횟수(숫자) * 문자열

문자열 연산에도 아래 복합대입연산을 적용할 수 있음

문자열 in 연산
문자열 내부에 어떤 문자열이 있는지 확인하려면 in 연산자를 사용할 수 있고, true/false를 반환해줌

문자열 인덱싱

• 문자열 내부적으로 보면 하나의 단어는 각각 하나의 인덱스(index)에 맵핑 될 수 있음

• 기본적인 인덱스는 0부터 시작되며, 해당 문자열의 길이-1까지 인덱스가 존재함
  “안녕하세요”는 길이가 5이므로, 인덱스는 0~4까지 가능
• 문자열을 받은 변수 혹은 문자열 자체에 대해서 인덱스를 대괄호[]와 함께 사용해서 접근할 수 있음
• 인덱스는 양수뿐만 아니라 음수도 가능함

문자열 슬라이싱

• 주어진 문자열에 대해서 특정 문자 1개에만 접근할 수 도 있지만, 문자열의 범위를 선택해야 하는 경우도 있음
  예 : 문자열의 두 번째 문자부터 다섯 번째 문자까지 선택하기
• 이렇게 부분 문자열을 추출하는 방법을 슬라이싱이라고 하며, 대괄호와 :을 통해서 표시할 수 있음
• 작성 방법: [ : ]  -> [부분 시작 문자의 인덱스 : 부분 끝 문자의 인덱스 + 1]
  예 : a[1:4] → 문자열 a의 부분 시작 문자의 인덱스 1부터
  부분 끝 문자의 인덱스 3 → “녕하세” 선택

생략 슬라이싱
• 대괄호 안에 넣는 숫자 둘 중 하나를 생략하여 사용할 수 있음
예 : [1:] [: 3]
• 뒤의 값 생략 시 가장 최대 위치 (마지막 글자)까지 지정
[1:] → [1:가장 마지막 글자 인덱스 + 1]
• 앞의 값 생략 시 가장 최소 위치 (첫번째 글자)부터 지정 [:3] → [0:가장 마지막 글자의 인덱스인 2 + 1]

• 슬라이싱에서도 인덱싱과 같이 음수도 가능
  • a[1:-2] → “녕하”
• 여기서도 뒷 인덱스는 원하는 끝 문자의 index보다 하나 커야 함
  부분 끝 문자의 인덱스 -3 + 1 = -2
  A[-5: -2] → “안녕하”

음수를 사용하는 슬라이싱에서도 앞/뒤 숫자 중 하나를 생략할 수 있음

뒤의 값 생략 시 가장 최대 위치 (마지막 글자)까지 지정 → a[-4:]
앞의 값 생략 시 가장 최소 위치 (첫번째 글자)부터 지정 → a[:-1]

슬라이싱시 아무런 숫자를 주지 않으면?
전체 문자열을 슬라이싱 함

문자열 관련 함수

문자열 길이 구하기

• len() 함수
• ()안에 문자열을 넣으면 주어진 문자열의 문자 개수(=문자열의 길이)를 계산해서 돌려줌
  예 : len(“안녕하세요”) → 5라는 숫자를 돌려줌
• 문자열에 공백이나 이스케이프 문자가 있을 경우 그것도 count하여 돌려줌

문자열 찾기

• find()라는 함수는 입력으로 주는 argument 문자가 처음 나타나는 위치(index 값)를 반환해주는 작업을 함

format() 함수

• “”로 묶인 문자열 안에 있는 중괄호{} 안의 문자가 format() 함수의 argument 로 주는 값으로 대치됨
  예 : “제 나이는 {} 살 입니다.”.format(20) → {} 대신 20으로 대치가 됨

대소문자 바꾸기

•  upper(), lower() 함수
• upper() 함수는 모든 알파벳을 대문자로 변환
• lower() 함수는 모든 알파벳을 소문자로 변환

문자열의 양 옆의 공백 제거하기

•  strip() 함수

문자열의 구성 파악하기

• isOO() → is가 붙어있기 때문에 True 혹은 False 반환
• isalnum(): 문자열이 알파벳 또는 숫자로만 구성되어 있는지 확인
• isalpha(): 문자열이 알파벳으로만 구성되어 있는지 확인
• islower(): 문자열이 모두 소문자로만 구성되어 있는지 확인
• isupper(): 문자열이 모두 대문자로만 구성되어 있는지 확인

문자열 자르기

• 문자열을 특정한 문자로 자르고 싶을 때 split() 함수를 사용
• default는 white space(공백)

자료형

파이썬에서의 자료형

• 프로그래밍을 할 때 쓰이는 숫자, 문자열 등 자료 형태로 사용하는 모든 것을 뜻함
• 프로그램의 기본이자 핵심 단위임
• C언어나 Java 같은 프로그래밍 언어와 달리, 파이썬에서는 코드를 작성할 때 프로그래머가 자료형을 지정하지 않아도 됨

프로그래밍 시 자료형을 지정하지 않아도 되긴 하지만, 파이썬 내부에서는 자동으로 자료형을 정해줌
• 런타임(실행 시간) 시에 자료형이 결정됨
• 자동으로 지정된 자료형은 어떻게 확인할 수 있나? -> type( )이라는 함수를 통해서 확인할 수 있음
• 실행시켜 보기 전에는 오류를 검출하기 어렵지만, 유연하고 빠르게 코딩이 가능

숫자형(수치 자료형)

• 숫자형(number)이란 숫자 형태로 이루어진 자료형으로, 123 같은 정수, 12.3 같은 실수, 2진수, 8진수, 16진수 등이 있음

정수를 2, 8, 16진법으로 변화할 수 있는 함수(메소드) 및 표현

정수(int, integer)와 실수(float, floating point)

• 정수와 2/8/16진법 사이의 변환처럼, 서로 다른 데이터 타입 사이의 변환이 가능함
• float(변수이름) → 변수이름의 자료형을 float로 변환
• int(변수이름) → 변수이름의 자료형을 int로 변환

정수와 문자열 사이의 형변환

• str(변수이름) → 변수이름의 자료형을 str로 변환

산술 연산자

정수/실수 혹은 실수/정수 나누기 값은 소수점을 포함할 수 있으므로 실수형 값 반환

관계 연산자

관계 연산자 적용에서도 정수(실수)와 문자형의 비교는 ‘같다’, ‘다르다’ 여부만 적용할 수 있음

복합대입연산자

• 연산과 할당을 합쳐놓은 것
• 식을 간결하게 표현할 수 있고, 변수가 이전에 가졌던 값을 수정하여 할당하는 일에 활용될 수 있음

연산자의 우선순위

• 괄호()가 가장 높은 우선순위를 갖음
• 곱셈 / 나눗셈 / 나머지 / 몫보다는 제곱이 더 높은 순위를 갖고, 할당/복합대입 연산이 가장 낮은 우선 순위를 갖음