![[알고리즘] 삽입 정렬과 빅 오(Big O)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcvWJOi%2FbtsrR6Z6pdA%2FAAAAAAAAAAAAAAAAAAAAAF6B_GEW9bQc7Qw6oBKMRqAFI28HgP7yyqoBlPIFxTrK%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DjmtOflQQGcm3FCQPd4bBfaFXx2s%253D)

이 글은 누구나 자료 구조와 알고리즘(저자 : 제이 웬그로우)의 내용을 개인적으로 정리하는 글임을 알립니다.
삽입 정렬
삽입 정렬의 수행 순서는 아래와 같다.
1. 첫 번째 패스스루에서 임시로 인덱스 1(두 번째 셀)의 값을 삭제하고 이 값을 임시 변수에 저장한다.
인덱스 1에 값이 없으므로 공백이 생긴다.

이후 각 패스스루마다 다음 인덱스의 값을 삭제한다.
2. 다음으로 공백 왼쪽에 있는 각 값을 가져와 임시 변수에 있는 값과 비교하는 시프트 단계를 시작한다.

공백 왼쪽에 있는 값이 임시 변수에 있는 값보다 크면 그 값을 오른쪽으로 시프트한다.

값을 오른쪽으로 시프트했으므로 자연히 공백이 왼쪽으로 옮겨진다.
임시로 삭제한 값보다 작은 값을 만나거나 배열의 왼쪽 끝에 도달해야 시프트 단계가 끝난다.
3. 임시로 제거한 값을 현재 공백에 삽입한다.

4. 1단계부터 3단계까지가 하나의 패스스루다. 배열의 마지막 인덱스에서 패스스루를 시작할 때까지 패스스루를 반복한다.
이때가 되면 배열은 완전히 정렬된다.
더 자세히 삽입 정렬 살펴보기
배열 [4, 2, 7, 1, 3]을 삽입 정렬 해보자.
첫 번째 패스스루 시작
인덱스 1의 값을 확인하며, 인덱스 1에 값 2가 들어 있다.

1단계 : 임시로 2를 삭제하고 temp_value라는 변수에 저장한다. 이를 표시하기 위해 나머지 배열의 윗부분으로 이 값을 옮기겠다.

2단계 : 4와 temp_value에 들어 있는 2를 비교한다.

3단계 : 4가 2보다 크므로 4를 오른쪽으로 시프트한다.

공백이 배열의 왼쪽 끝에 있으므로 더 이상 왼쪽으로 시프트할 수 없다.
4단계 : temp_value를 다시 배열에 삽입해서 첫 번째 패스스루를 끝낸다.
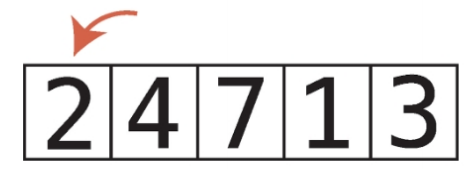
두 번째 패스스루 시작
5단계 : 두 번째 패스스루에서는 인덱스 2의 값을 임시로 삭제한다. 이 값을 temp_value에 저장한다. 이때 temp_value는 7이다.

6단계 : 4와 temp_value를 비교한다.

4가 더 작으므로 시프트하지 않는다. temp_value보다 작은 값에 도달했으므로 시프트 단계를 끝낸다.
7단계 : temp_valule를 다시 공백에 삽입하고 두 번째 패스스루를 끝낸다.

세 번째 패스스루
8단계 : 임시로 1을 삭제하고 temp_value에 저장한다.
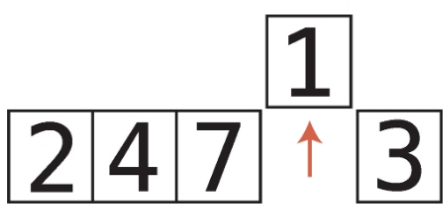
9단계 : 7과 temp_value를 비교한다.

10단계 : 7은 1보다 크므로 7을 오른쪽으로 시프트한다.
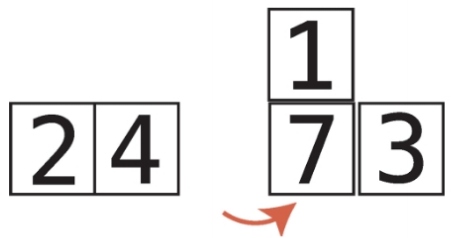
11단계 : 4와 temp_value를 비교한다.
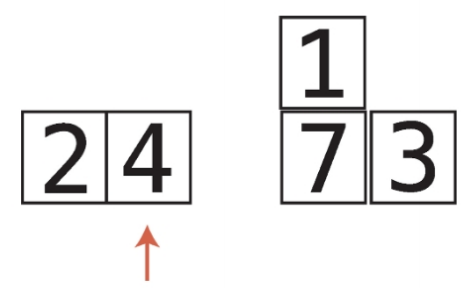
12단계 : 4는 1보다 크므로 마찬가지로 시프트한다.
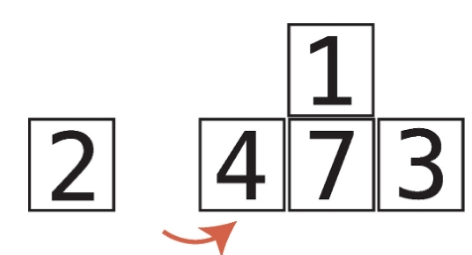
13단계 : 2와 temp_value를 비교한다.

14단계 : 2가 더 크므로 시프트한다.
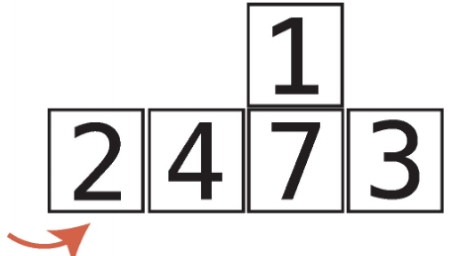
15단계 : 공백이 배열의 왼쪽 끝에 있으므로 temp_value를 공백에 삽입하고 패스스루를 끝낸다.

네 번째 패스스루 시작
16단계 : 임시로 인덱스 4의 값을 삭제하고 temp_value에 저장한다. 값은 3이다.

17단계 : 7과 temp_value를 비교한다.
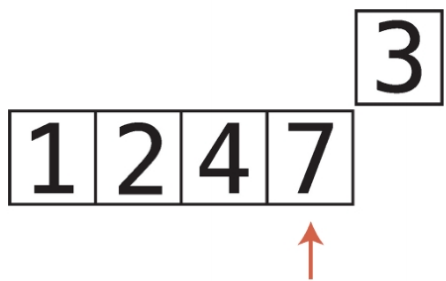
18단계 : 7이 더 크므로 7을 오른쪽으로 시프트한다.

19단계 : 4와 temp_value를 비교한다.

20단계 : 4가 3보다 크므로 4를 시프트한다.
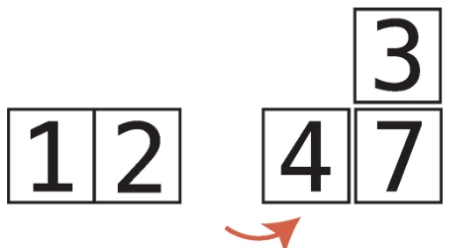
21단계 : 2와 temp_value를 비교한다. 2는 3보다 작으므로 시프트 단계를 끝낸다.

22단계 : temp_value를 다시 공백에 삽입한다.

이제 배열이 완전히 정렬되었다.

삽입 정렬의 효율성
삽입 정렬에 포함된 단계는 삭제, 비교, 시프트, 삽입 네 종류다.
먼저 비교를 살펴보면, 비교는 공백 왼쪽에 있는 값과 temp_value를 비교할 때마다 일어난다.
배열이 역순으로 정렬된 최악의 시나리오라면 각 패스스루마다 temp_value 왼쪽에 있는 모든 값을 비교해야 한다.
따라서 각 패스스루는 공백이 배열의 왼쪽 끝으로 가야만 끝난다.
원소가 5개인 배열에서는 비교가 1 + 2 + 3 + 4 = 10번의 비교가 일어났다.
따라서 데이터가 N개 있으면 비교는 1 + 2 + 3 + ... + N-1 개의 비교가 일어난다.
- 원소가 10개면 45번의 비교
- 원소가 20개면 190번의 비교
- 이러한 패턴에 따르면 결국 원소가 N개인 배열일 때 대략 N² / 2 번의 비교가 일어난다.
시프트는 값을 한 셀 오른쪽으로 옮길 때마다 일어난다.
배열이 역순으로 정렬돼 있다면 비교가 일어날 때마다 값을 오른쪽으로 시프트해야 하므로 비교 횟수만큼 시프트가 일어난다.
최악의 시나리오에서 비교와 시프트 횟수를 합치면 아래와 같다.

배열로부터 temp_value를 삭제하고 다시 삽입하는 작업은 패스스루당 한 번 일어난다.
패스스루는 항상 N-1번이므로 결국 N-1번의 삭제와 N-1번의 삽입이 있을 것이다.
따라서 총 합은 아래와 같다.

총 N² + 2N -2 단계가 걸리는 것을 알았는데, 이것을 빅 오로 O(N² + 2N -2) 이렇게 표현하면 안된다.
아래의 빅 오 표기법의 규칙을 따라야 하기 때문이다.
- 빅 오 표기법은 상수를 무시한다.
- 빅 오 표기법은 다양한 차수가 한데 섞여 있을 때 빅 오 표기법은 가장 높은 차수의 N만 고려한다.
때문에 삽입 정렬을 빅 오로 표현하면 O(N²)이다.
왜 가장 높은 차수의 N만 고려하는지는 아래와 같다.
| N | N² | N³ | N⁴ |
| 2 | 4 | 8 | 16 |
| 5 | 25 | 125 | 625 |
| 10 | 100 | 1,000 | 10,000 |
| 10 | 10,000 | 1,000,000 | 100,000,000 |
N이 증가할수록 어떤 N 차수보다 N⁴의 비중이 훨씬 더 커져서 작은 차수는 미미해 보인다.
표 가장 아랫줄에 나오는 N⁴+N³+N²+N를 모두 더하면 총 101,010,100이다.
내림을 하면 100,000,000이 되어 낮은 차수의 N을 무시한 것과 같다.
버블, 선택, 삽입 정렬 모두 O(N²)이지만 버블 정렬은 N²단계인데 반해 선택 정렬은 N² / 2단계로 선택 정렬이 빨랐다.
삽입 정렬 역시 N²단계가 걸리므로 언뜻 보기에는 버블 정렬만큼 느리다고 할 수 있다.
하지만 삽입 정렬 보다 두 배 더 빠른 선택 정렬이 이 셋 중 가장 나은 방법이라고 생각하는 것은 옳지 않다.
평균적인 경우
최악의 시나리오에서는 선택 정렬이 삽입 정렬보다 빠른게 사실이다.
하지만 평균 시나리오도 중요하게 고려해야 한다.
정의에 따르면 가장 자주 일어나는 경우가 평균 시나리오다.

최선, 최악의 시나리오는 상대적으로 드물게 발생한다.
실제로는 대부분 평균 시나리오가 일어난다.
완벽하게 오름차순 또는 내림차순으로 정렬된 데이터는 드물기 때문이다.
선택 정렬을 최선, 평균, 최악의 시나리오대로 비교하면 아래와 같다.
[1, 2, 3, 4]는 이미 정렬된 최선의 경우다.
같은 데이터에 대해 최악의 경우는 [4, 3, 2, 1]일 것이며, 평균적인 경우라면 [1, 3, 4, 2]등일 것이다.
- 최악의 경우 : 6번의 비교와 6번의 시프트 총 12단계
- 평균적인 경우 : 4번의 비교와 2번의 시프트 총 6단계
- 최선의 경우 : 3번의 비교와 0번의 시프트 총 3단계
삽입 정렬은 시나리오에 따라 성능이 크게 좌우된다.
선택 정렬과 삽입 정렬을 최선, 평균, 최악의 시나리오에서 단계를 비교하면 아래와 같다.

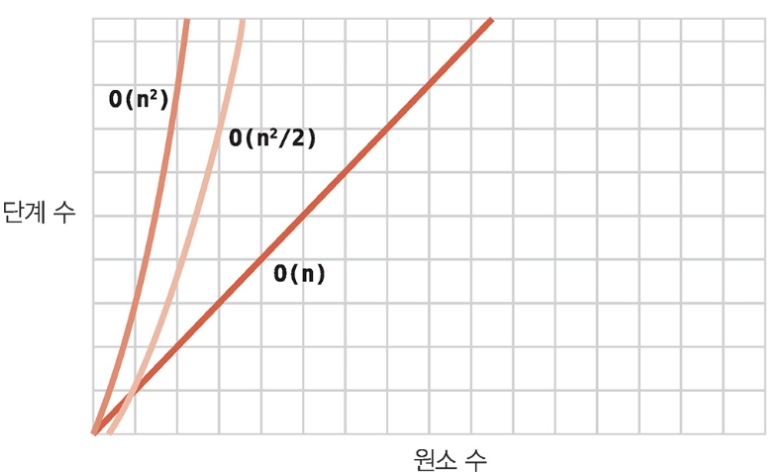
최선의 시나리오 즉, 배열이 정렬되어있다면 선택 정렬을 사용하는 것이 더 효율적이고, 평균적인 경우 즉, 배열이 임의로 나열되어 있다면 선택 정렬이나 삽입 정렬의 효율은 같고, 최악의 경우 즉, 배열이 역순으로 정렬되어 있다면 선택 정렬이 더 효율적이다.
- 최선의 시나리오 : 삽입 정렬이 더 효율적
- 평균의 시나리오 : 둘 다 효율성 비슷함
- 최악의 시나리오 : 선택 정렬이 더 효율적
'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [Java] 라빈-카프 문자열 탐색 알고리즘 (2) | 2023.11.25 |
|---|---|
| [알고리즘] 코드 효율성과 빅 오(Big O) (1) | 2023.09.02 |
| [알고리즘] 선택 정렬과 빅 오(Big O) (0) | 2023.08.31 |
| [알고리즘] 버블 정렬과 빅 오(Big O) (0) | 2023.08.30 |
| [Java] 8퀸 문제(분기한정법) (0) | 2023.08.29 |
![[Java] 라빈-카프 문자열 탐색 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbJ4KpK%2FbtsAWgyYdpc%2FAAAAAAAAAAAAAAAAAAAAAIASjTnObLb3xhFl_D-IuOsBHXYc4LvGsm53YozhMSwJ%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DbkTsvCVZVXMgb4Dxot%252BeD70bffM%253D)
![[알고리즘] 코드 효율성과 빅 오(Big O)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FFqMIm%2FbtsrS42TZo5%2FAAAAAAAAAAAAAAAAAAAAABClMUd2TIL4twq-C0aNcZgrDNm13hJraPmdxm0iLgeo%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Dgg9t3H1jpkJM8mDNPOXVRFvA%252Beo%253D)
![[알고리즘] 선택 정렬과 빅 오(Big O)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb5okfE%2FbtsrCnPO2Lg%2FAAAAAAAAAAAAAAAAAAAAAPKV8HAtzgaeKOSTrUx-qLAJ7GJsFeFFvNErtpaXfDZ2%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Duu1%252FjSuO8N3pzBnhEF3%252FmNQsvnQ%253D)
![[알고리즘] 버블 정렬과 빅 오(Big O)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcZL7Iu%2FbtsrDcmeIsi%2FAAAAAAAAAAAAAAAAAAAAAHiwFvMb2x1oa9XRCLQDtqwnjSKL8W4YixX4CACfYLN_%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DLeM2521NIPi1JiZnHuVOcDBvO8s%253D)