Do it! 자료구조와 함께 배우는 알고리즘 입문[자바편] 연습문제와 실습문제입니다.
8퀸 문제란?
- 서로 공격하여 잡을 수 없도록 8개의 퀸을 8x8 체스판에 놓는 것
퀸은 현재 놓여있는 지점에서 가로 or 세로 or 대각선의 8가지 방향으로 직선 이동 가능하다.
체스판의 가로줄을 행, 세로줄을 열이라 하고 배열 인덱스에 맞추어 행과 열에 0~7의 번호를 부여한다.
이 문제의 답이 되는 조합은 92가지이다.
아래의 그림은 92가지중 하나의 조합을 나타낸 것이다.
퀸 배치하기
8개의 퀸을 체스판 64칸(8*8)이므로 처음에 64칸중 아무칸에 놓고, 다음 퀸을 배치할 때는 나머지 63칸에서 임의로 선택한다.
- 64 x 63 x 62 x 61 x 60 x 59 x 58 x 57 = 178,462,987,637,760
이 조합을 모두 나열하고 각각의 조합이 8퀸 문제의 조건을 만족하는지 조사하는 것은 현실적이지 않다.
따라서 규칙 하나를 세운다.
- 규칙1 : 각 열에 퀸을 1개만 배치한다.
이러면 퀸을 배치하는 조합의 수는 16,777,216가지로 많이 줄어들지만 아직도 여전히 많다.
그렇기에 규칙 하나를 더 추가한다.
- 규칙2 : 각 행에 퀸을 1개만 배치한다.
아래의 그림은 규칙1과 규칙2를 모두 만족하는 배치의 일부(4가지)를 나타낸 것이다.
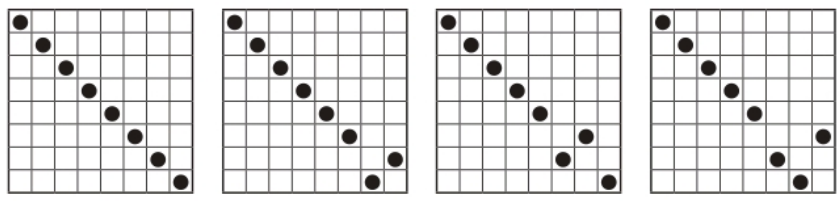
이렇게 하면 이 조합을 나열하는 알고리즘을 어떻게든 만들 수 있다.
하지만 그렇게 간단히 만들어 지지는 않는다.
이제 문제를 정리하기 위해 처음으로 다시 돌아가 규칙 1에 따라 조합을 나열하는 알고리즘을 생각하면
모든 열에 퀸이 아직 배치되지 않은 상태이다.
첫 번째 열에 퀸을 배치하는 경우의 수는 8개이다.
두 번째 열에 퀸을 배치하는 경우의 수 또한 8개이다.
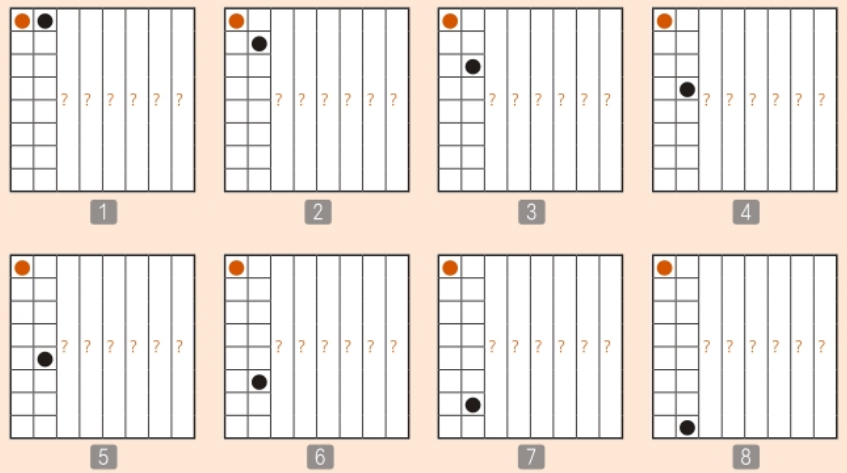
여기서 규칙2를 적용해서 같은 행에 여러 퀸을 배치하는 조합은 없애버리자.
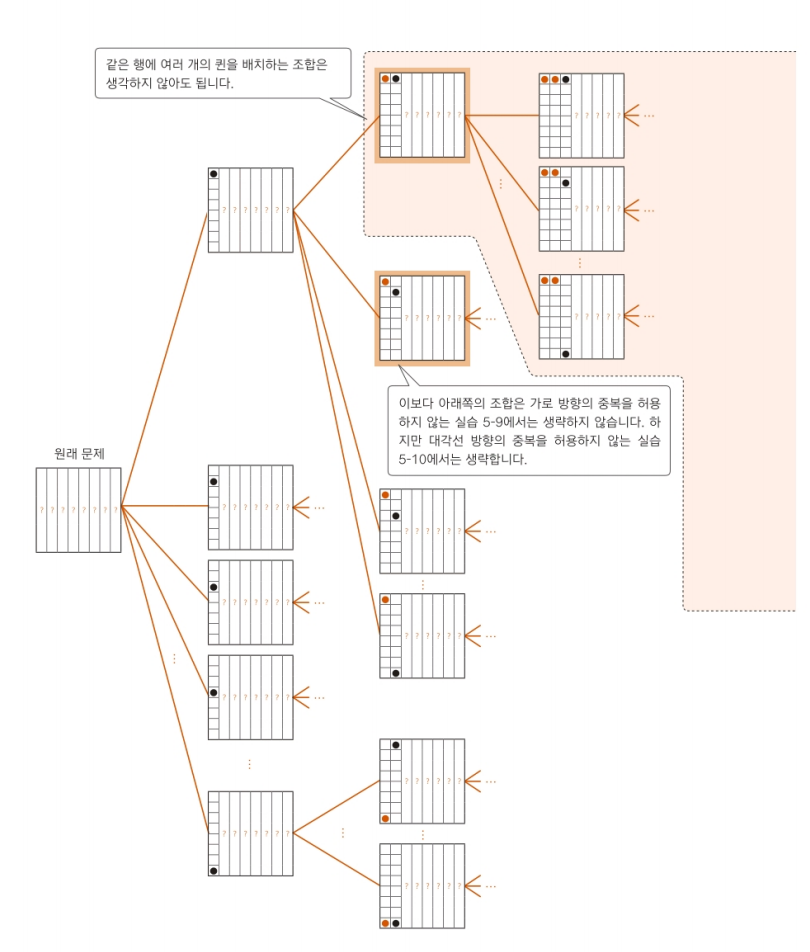
분기 조작(규칙 1)
분기란 가지가 뻗어 나가듯이 문제를 나누어 푸는 과정을 의미
또한 지금은 모든 조합만 나열하고, 8퀸 문제 해결은 마지막에 다룬다.
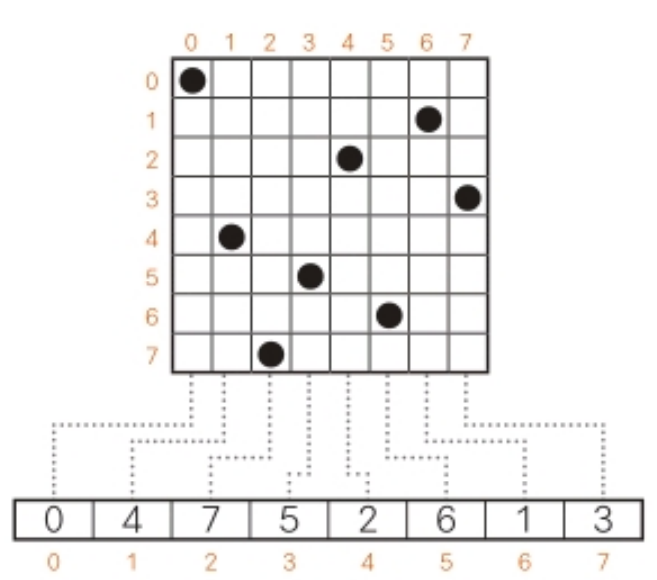
배열 pos는 퀸의 배치를 나타낸다.
i열에 놓인 퀸의 위치가 j행이면 pos[i]의 값을 j로 한다.
즉, pos[1]의 값이 4이면 1열의 퀸이 4행에 배치된 상태를 의미한다.
set 메소드는 pos[i]에 0부터 7까지의 값을 순서대로 대입하여 i열에 퀸을 1개만 배치하는 8가지 조합을 만드는 재귀 메소드이다.
매개변수 i가 이 퀸을 배치할 열이다.
class QueenB {
static int[] pos = new int[8]; // 각 열의 퀸의 위치
//--- 각 열의 퀸의 위치를 출력 ---//
static void print() {
for (int i = 0; i < 8; i++)
System.out.printf("%2d", pos[i]);
System.out.println();
}
//--- i열에 퀸을 배치 ---//
static void set(int i) {
for (int j = 0; j < 8; j++) {
pos[i] = j; // 퀸을 j행에 배치함
if (i == 7) // 모든 열에 배치함
print();
else
set(i + 1); // 다음 열에 퀸을 배치
}
}
public static void main(String[] args) {
set(0); // 0 열에 퀸을 배치
}
}이렇게 하면 규칙1을 적용한 것과 같이 16,777,216가지의 조합이 모두 나열된다.
이런 방법을 분기 조작 또는 가지 뻗기라고 한다.
분기 한정법(규칙 1 + 규칙 2)
class Main{
static boolean[] flag = new boolean[8]; // 각 행에 퀸이 이미 배치되었는가?
static int[] pos = new int[8]; // 각 열의 퀸의 위치
//--- 각 열의 퀸의 위치를 출력 ---//
static void print() {
for (int i = 0; i < 8; i++)
System.out.printf("%2d", pos[i]);
System.out.println();
}
//--- i열의 알맞은 위치에 퀸을 배치 ---//
static void set(int i) {
for (int j = 0; j < 8; j++) {
if (flag[j] == false) { // j 행에 퀸을 아직 배치하지 않음
pos[i] = j; // 퀸을 j행에 배치함
if (i == 7) // 모든 열에 배치함
print();
else {
flag[j] = true;
set(i + 1);
flag[j] = false;
}
}
}
}
public static void main(String[] args) {
set(0);
}
}위 알고리즘에서는 flag라는 배열을 사용한다.
flag는 같은 행에 중복하여 퀸이 배치되는 것을 방지하기 위한 표시이다.
j행에 퀸을 배치하면 flag[j]의 값을 true로 하고, 배치되지 않은 상탯값은 false로 설정한다.
set(i + 1) 메소드 실행이 끝나면 다음 경우의 수를 위해 퀸을 j행에서 제거한다(flag[j] = false)
set 메소드에서는 퀸을 아직 배치하지 않은 행에만 퀸을 배치한다.
이렇게 필요하지 않은 분기를 없애 불필요한 조합을 줄이는 방법을 한정 조작이라 하고, 분기 조작과 한정 조작을 조합하여 문제를 풀어가는 방법을 분기 한정법이라고 한다.
아직까지는 퀸이 행 방향과 열 방향으로 겹쳐지지 않는 조합을 나열하기만 한 것이다.
퀸은 대각선 방향으로도 이동할 수 있기 때문에 어떤 대각선에서 보더라도 퀸을 1개만 배치하는 한정 조작을 추가해야 한다.
8퀸 문제 해결 코드
class Main {
static boolean[] flag_a = new boolean[8]; // 각 행에 퀸이 이미 배치되었는가?
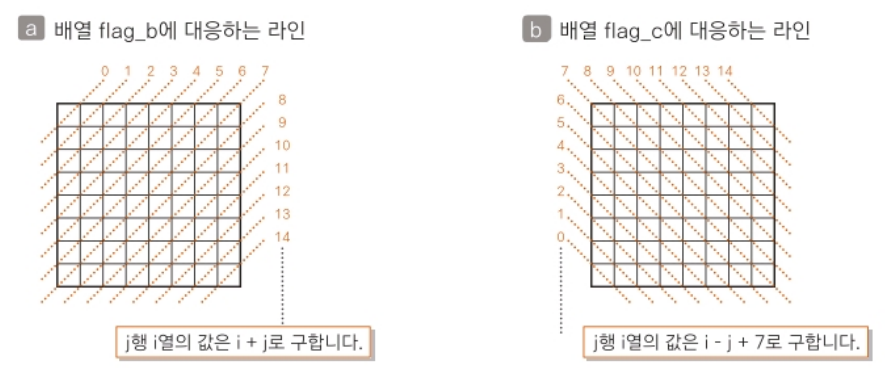
static boolean[] flag_b = new boolean[15]; // 대각선 ↙에 퀸이 이미 배치되었는가?
static boolean[] flag_c = new boolean[15]; // 대각선 ↘에 퀸이 이미 배치되었는가?
static int[] pos = new int[8]; // 각 열의 퀸의 위치
//--- 각 열의 퀸의 위치를 출력 ---//
static void print() {
for (int i = 0; i < 8; i++)
System.out.printf("%2d", pos[i]);
System.out.println();
}
//--- i열의 알맞은 위치에 퀸을 배치 ---//
static void set(int i) {
for (int j = 0; j < 8; j++)
{
if (flag_a[j] == false && // 가로(j행)에 아직 배치하지 않음
flag_b[i + j] == false && // 대각선 ↙에 아직 배치하지 않음
flag_c[i - j + 7] == false) // 대각선 ↘에 아직 배치하지 않음
{
pos[i] = j; // 퀸을 j행에 배치함
if (i == 7) print();
else
{
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true;
set(i + 1);
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false;
}
}
}
}
public static void main(String[] args) {
set(0);
}
}- flag_b와 flag_c는 / 방향과 \방향의 대각선 위에 퀸을 배치했는지 체크하는 배열이다.
print 메소드를 수정하여 아래의 그림과 같이 퀸의 배치 상황을 출력하는 메소드를 작성class Main { static boolean[] flag_a = new boolean[8]; // 각행에 퀸을 배치했는지 체크 static boolean[] flag_b = new boolean[15]; // /대각선에 퀸을 배치했는지 체크 static boolean[] flag_c = new boolean[15]; // ＼대각선에 퀸을 배치했는지 체크 static int[] pos = new int[8]; // 각열의 퀸의 위치 //--- 배치 상황(각열의 퀸의 위치)을 출력 ---// static void print() { for (int i = 0; i < 8; i++) { for (int j = 0; j < 8; j++) System.out.printf("%s", j == pos[i] ? "■" : "□"); System.out.println(); } System.out.println(); } //--- i열의 알맞은 위치에 퀸을 배치 ---// static void set(int i) { for (int j = 0; j < 8; j++) { if (flag_a[j] == false && // 가로(j행)에 미배치 flag_b[i + j] == false && // /대각선에 미배치 flag_c[i - j + 7] == false) { // ＼대각선에 미배치 pos[i] = j; // 퀸을 j행에 배치 if (i == 7) // 모든 열에 배치 마침 print(); else { flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true; set(i + 1); flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false; } } } } public static void main(String[] args) { set(0); } }
8퀸 문제를 비재귀적으로 구현
class Main { static boolean[] flag_a = new boolean[8]; // 각행에 퀸을 배치했는지 체크 static boolean[] flag_b = new boolean[15]; // /대각선에 퀸을 배치했는지 체크 static boolean[] flag_c = new boolean[15]; // ＼대각선에 퀸을 배치했는지 체크 static int[] pos = new int[8]; // 각열의 퀸의 위치 //--- 배치 상황(각열의 퀸의 위치)을 출력 ---// static void print() { for (int i = 0; i < 8; i++) { for (int j = 0; j < 8; j++) System.out.printf("%s", j == pos[i] ? "■" : "□"); System.out.println(); } System.out.println(); } //--- i열의 알맞은 위치에 퀸을 배치 ---// static void set(int i) { int j; int[] jstk = new int[8]; Start : while (true) { j = 0; while (true) { while (j < 8) { if (!flag_a[j] && !flag_b[i + j] && !flag_c[i - j + 7]) { pos[i] = j; if (i == 7) // 모든 열에 배치종료 print(); else { flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = true; jstk[i++] = j; // i열의 행을 Push continue Start; } } j++; } if (--i == -1) return; j = jstk[i]; // i열의 행을 Pop flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = false; j++; } } } public static void main(String[] args) { set(0); } }
'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 선택 정렬과 빅 오(Big O) (0) | 2023.08.31 |
|---|---|
| [알고리즘] 버블 정렬과 빅 오(Big O) (0) | 2023.08.30 |
| [Java] 재귀 알고리즘 메모화 (1) | 2023.08.28 |
| [알고리즘] 빅 오 (Big O) 표기법 (0) | 2023.08.27 |
| [알고리즘] 이진 탐색 (0) | 2023.08.12 |