![[알고리즘] 다익스트라(Dijkstra) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbOn2C3%2FbtsB7iQsnIl%2FAAAAAAAAAAAAAAAAAAAAAIUsBzwq1gPXP-c-2IkY-BSs69qllGFNPoK3vfLBZF98%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DNY7%252FUEjzSotudr3cEtr52n0l%252B%252FI%253D)

이 글은 이것이 자료구조+알고리즘이다 with C 언어(저자:박상현) 책 내용을 개인적으로 정리하는 글임을 알립니다.
다익스트라 알고리즘의 개념
다익스트라 알고리즘은 여러가지 경로중에 목적지에 도착하기 위해 가장 빠른 경로를 찾아주는 알고리즘이다.
프림 알고리즘이 단순히 간선의 길이를 이용하여 어떤 간선을 먼저 연결할지 결정하는 데 비해 데이크스트라 알고리즘은 경로의 길이를 감안해서 간선을 연결, 데이크스트라 알고리즘의 경우 사이클이 없는 방향성 그래프에 한해서만 사용 가능
다익스트라 알고리즘 동작 방식
❶ : 각 정점에는 시작점으로부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비하고 각 정점에 대한 경로의 길이를 ∞(무한대)로 초기화
❷ : 시작 정점의 경로 길이를 0으로 초기화하고(시작 정점에서 시작 정점까지의 거리는 0이므로) 최단 경로에 추가
❸ : 최단 경로에 새로 추가된 정점의 인접 정점에 대해 경로 길이를 갱신하고 이들을 최단 경로에 추가
- 만약 추가하려는 인접 정점이 이미 최단 경로 안에 있다면, 갱신되기 이전의 경로 길이가 새로운 경로 길이보다 더 큰 경우에 한해 다른 선행 정점을 지나던 기존 경로가 현재 정점을 경유하도록 수정
❹ : 그래프 내의 모든 정점이 최단 경로에 소속될 때까지 단계 ❸의 과정을 반복
예제
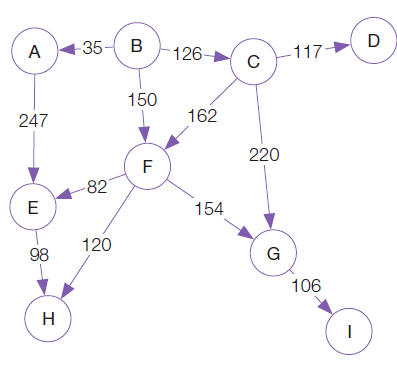
B를 시작점으로 설정하고 ‘나머지 모든 정점’을 도착점으로 지정
각 정점별로 경로 길이를 정점 좌측 상단의 상자 안에 표시하고 초깃값을 무한대로 설정
시작 정점 B의 경로 길이는 0으로 수정(B에서 B로 가는 비용은 0이므로)

시작 정점인 B에 인접한 정점들을 찾고 간선의 가중치를 조사
현재 경로 B-A 사이의 가중치는 경로 길이인 ∞보다 작으므로 A의 경로 길이를 35로 수정
같은 방법으로 경로 B-C의 경로 길이는 126, B-F의 경로 길이는 150으로 수정

A의 경로 길이 35와 간선 A-E의 비용 247을 더한 값 282를 경로 길이로 입력

C의 인접 정점은 D, F, G
현재 D의 경로 길이는 무한대이므로 B-C-D 경로의 비용(126+117=243)을 그대로 입력
G 역시 경로 길이가 무한대이므로 B-C-G 경로의 비용(126+220=346)을 입력
새로 발견한 경로 B-C-F는 B-F보다 비용이 크기 때문에 채택할 수 없음

F에 인접한 정점은 E, G, H
E정점으로 가는 기존 경로인 B-A-E는 경로 길이가 282인데 새로운 경로인 B-F-E의 비용이 232로 더 작으므로 기존의 경로 B-A-E는 폐기하고 새로운 경로 B-F-E를 채택
G도 마찬가지로 기존 B-C-G(비용 346)보다 새 경로 B-F-G(비용 304)가 저렴하므로 예전 것을 폐기하고 새 경로를 채택
H의 경로 길이는 현재 무한대이므로 경로 B-F-H의 비용 270을 H의 경로 길이로 입력

E에 인접한 정점 H가 있기는 하지만 경로 B-F-E-H의 비용이 330이고 현재 경로(B-F-H) 길이 270보다 크므로 무시한다.
정점 G만 유일하게 방문하지 않은 정점 I를 가지고 있다.
I의 현재 경로 길이는 무한대이므로 경로 B-F-G-I의 비용 410을 입력한다.

이제 더 탐사할 노드가 없으므로 최단 경로 탐색을 종료한다.
각 정점의 상단에 있는 상자 속 값들은 B에서부터 해당 정점에 이르는 경로상 모든 간선의 가중치이다.

'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [Java] 문자열 탐색(브루트 포스, KMP, 보이어 무어) (0) | 2024.01.15 |
|---|---|
| [Java] 정렬 알고리즘(Sorting Algorithm) (1) | 2024.01.15 |
| [알고리즘] 최소 신장 트리(Minimum Spanning Tree) (1) | 2023.12.18 |
| [알고리즘] 그래프 위상 정렬(Topological sorting) (1) | 2023.12.17 |
| [알고리즘]보이어-무어(Boyer-Moore) 문자열 탐색 알고리즘 (1) | 2023.11.29 |
![[Java] 문자열 탐색(브루트 포스, KMP, 보이어 무어)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcbLQuY%2FbtsDpvWt1Va%2FAAAAAAAAAAAAAAAAAAAAAHMgeOwbkg-ECg8HHqXlwGiLNERUU61NmMbG3x7VWA6-%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DqLhPdx9FTeQvVo3UqY6kDitfIL0%253D)
![[Java] 정렬 알고리즘(Sorting Algorithm)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbJeL4L%2FbtsDrFJ2NxR%2FAAAAAAAAAAAAAAAAAAAAAIG6b6UhMLwhZHx68HohHPPaWrnyvRg5Ewuv3cEGgaKM%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Dz84o8%252BnDxl1vHQzq8MZA%252FjJkE3s%253D)
![[알고리즘] 최소 신장 트리(Minimum Spanning Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fd1qQoN%2FbtsB3uxF8xX%2FAAAAAAAAAAAAAAAAAAAAAC-zp5et6VPskAKFVeeCNgJTkSN_gPNX7A59uFkuNL2l%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DY4xWhWdGeTIP0vYP67hSUwatX64%253D)
![[알고리즘] 그래프 위상 정렬(Topological sorting)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fr4M3a%2FbtsB17QpJRA%2FAAAAAAAAAAAAAAAAAAAAAIMpC4Km5pPLFh1MmeIcFsTqX8qolOnDvydRca4gqirV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Db5FM0Da99kTJW4MoaYifiw2Ttz0%253D)