이 글은 이것이 자료구조+알고리즘이다 with C 언어(저자:박상현) 책 내용을 개인적으로 정리하는 글임을 알립니다.
최소 신장 트리
가중치 그래프
- 가중치 그래프 : 그래프에서 정점과 정점을 잇는 간선을 지나기 위해 가중치라는 새로운 속성을 부여한 그래프
신장 트리(Spanning Tree)
모든 정점을 연결하는 트리
신장 트리는 그래프의 하위 개념
모든 정점을 연결하는 그래프(네트워크 그래프)에서 사이클이 되는 간선을 제거하면 신장 트리가 된다.
따라서 n개의 정점을 정확히 (n-1)개의 간선으로 연결한다.
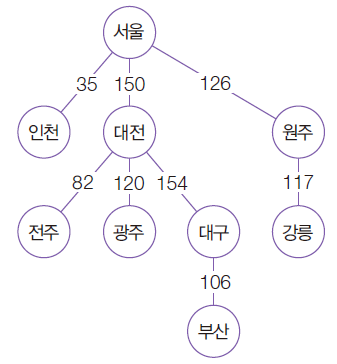
최소 신장 트리
최소 신장 트리는 최소 가중치 신장 트리라고 부르기도 한다.
최소 신장 트리는 그래프의 모든 정점을 최소 비용으로 연결하는 부분 그래프 또는 트리의 모든 노드를 최소 비용으로 연결하는 트리라고 말할 수 있다.
최소 신장 트리 알고리즘에는 아래와 같은 종류가 있다.
- 프림(Prim) 알고리즘
- 크루스칼(Kruskal) 알고리즘
프림 알고리즘
프림 알고리즘의 최소 신장 트리 생성 과정
❶ : 그래프와 최소 신장 트리를 준비 – 이때의 최소 신장 트리는 노드가 하나도 없는 상태
❷ : 그래프에서 임의의 정점을 시작 정점으로 선택하여 최소 신장 트리의 뿌리 노드로 삽입
❸ : 최소 신장 트리에 삽입된 정점들과 이 정점들의 모든 인접 정점 사이에 있는 간선의 가중치를 조사
- 간선 중에 가장 가중치가 작은 것을 골라 이 간선에 연결된 인접 정점을 최소 신장 트리에 삽입
- 단, 새로 삽입되는 정점은 최소 신장 트리에 삽입된 기존 노드와 사이클을 형성해서는 안 됨
❹ : ❸의 과정을 반복하다가 최소 신장 트리가 그래프의 모든 정점을 연결하게 되면 알고리즘을 종료
예시
시작 정점을 정해야 한다.
어느 것을 골라도 무관하지만 B를 시작 정점으로 선택
B는 시작 정점으로 선택됨과 동시에 최소 신장 트리의 뿌리노드가 된다.
정점 B에 연결된 간선은 B-A, B-C, B-F 3개임
가장 가중치가 작은 간선은 가중치가 35인 B-A이므로 A를 최소 신장 트리에 추가
최소 신장 트리에 연결된 노드는B, A
B, A에 연결된 간선은 B-C, B-F, A-E
B-C의 가중치가 126으로 가장 작기 때문에 C를 최소 신장 트리에 추가
최소 신장 트리의 노드는 모두 3개가 되었고, 조사해야 할 간선이 4개가 되었음
C-F간선은 사이클을 형성하기 때문에 조사해야 할 간선에서 제외 (B-F와 C-F 둘 중 하나를 제외하면 되지만, 가중치가 큰 간선 제외함)
가중치를 조사할 간선은 모두 4개(C-D, B-F, C-G, A-E)
이 중 가장 가중치가 작은 간선은 C-D(117)이므로 D를 최소 신장 트리에 추가
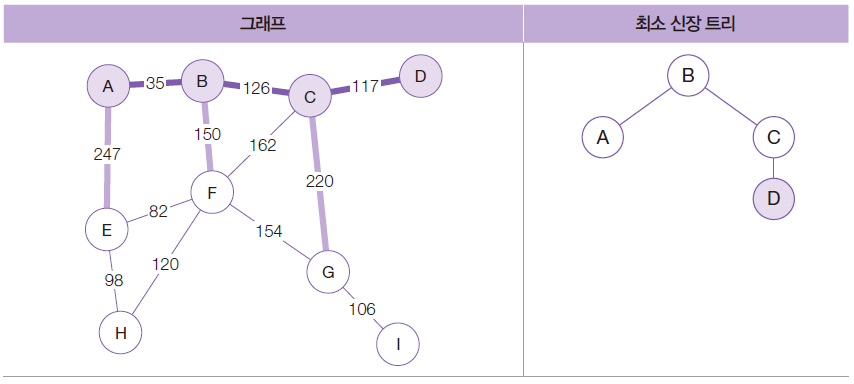
간선 B-F, C-G, A-E 중 가중치가 가장 작은 간선은 B-F(150)
F를 최소 신장 트리에 추가
F가 최소 신장 트리에 추가됨으로써 조사 대상 간선에 변화가 생김
A-E간선은 가중치가 더 작은 F-E간선에 의해, C-G간선은 F-G간선에 의해 조사 대상에서 제거됨
F-H 간선이 조사 대상으로 새로 추가됨
간선 3개(F-E, F-G, F-H) 중 가장 작은 가중치를 갖는 간선은 F-E(82)이므로 이를 최소 신장 트리에 추가
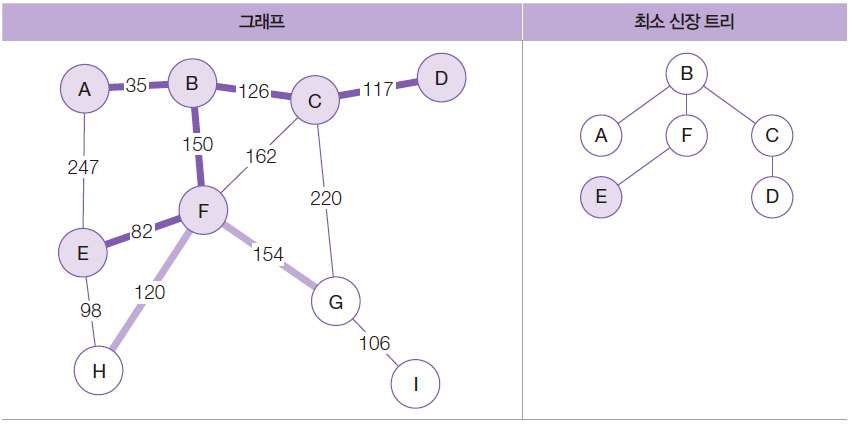
F-H 간선이 E-H 간선에 의해 조사 대상에서 제거
조사 대상인 2개 (E-H, F-G)의 간선 중 가중치가 가장 적은 간선은 E-H(98)
최소 신장 트리에 H를 추가
조사 대상 간선이 F-G 하나만 남았으므로 이 간선을 선택하고 G를 최소 신장 트리에 추가
조사 대상 간선이 G-I 하나임, 정점 I를 최소 신장 트리에 추가
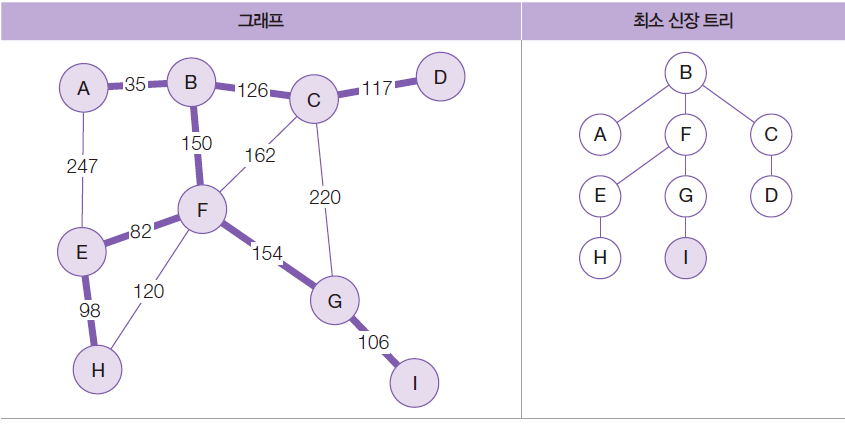
프림 알고리즘 구현 시 고려할 사항
어떤 자료구조를 최소 신장 트리에 사용할 것인 지의 판단
- 자료구조는 배열, 링크드 리스트, 트리, 그래프 등 다양
조사 대상 간선 중 최소 가중치를 가진 것을 골라내는 과정에서 발생하는 성능 문제
- 최소 신장 트리에 정점이 하나 추가될 때마다 그 수가 늘어나거나 줄어드는 조사 대상 간선 집합 속에서 ‘최소 가중치’를 가진 간선을 찾는 과정에서 성능 문제 발생
- 그래프에 정점이 N개 존재한다고 가정하면 정점 추가 작업을 N회 해야 하고, 정점을 추가할 때마다 그래프 내
정점 N개를 순회해야 하므로 N×N회, 즉 N²회 반복 처리가 필요
삽입과 삭제가 빠르고 최솟값을 찾는 데 비용도 거의 들지 않는 우선순위 큐를 이용하는 것이 가장 적절
크루스칼 알고리즘
크루스칼 알고리즘은 그래프 내 모든 간선의 가중치 정보를 사전에 파악하고, 이 정보를 토대로 최소 신장 트리를 구축해 나간다.
파란색 간선은 현재 집합 S에서 선택한 간선
빨간색 간선은 집합 S에서 선택한 간선을 숲 F에 추가한 간선이다.
크루스칼 알고리즘 작동 순서
❶ : 그래프 내의 모든 간선을 가중치의 오름차순으로 정렬하여 목록을 생성
❷ : ❶에서 만든 간선의 목록을 차례대로 순회하면서 간선을 최소 신장 트리에 추가
- 단, 이때 추가된 간선으로 인해 최소 신장 트리 내에 사이클이 형성되면 안 됨
사이클 형성 방지
크루스칼 알고리즘에서 중요한 점은 '사이클 형성을 어떻게 방지할 것인가?'이다.
DFS를 통해 사이클을 방지할 수도 있다.
이미 방문했던 노드를 또 만난다면 사이클이 있다는 뜻이기 때문이다.
DFS를 이용한 방법은 탐색 비용이 크다는 단점이 있다.
이 방법의 대안으로 분리 집합을 이용하는 방법이 있다.
- 각 정점별로 각각의 분리 집합을 만들고, 간선으로 연결된 정점들에 대해서는 합집합 수행.
- 간선으로 연결할 두 정점이 같은 집합에 속해 있다면 이 연결은 사이클을 이루게 되기에 연결하지 않음
예를 들어, A와 D를 연결한다고 가정하자
아래의 왼쪽은 정점 A와 D가 별개의 집합 속에 있기 때문에 사이클을 이루지 않는다.
오른쪽은 A와 D가 같은 집합에 속해있고, A와 D를 이으면 사이클이 생긴다.
따라서 서로 다른 집합에 속해있는 정점들만 연결하면 사이클이 생기지 않는다.
예제
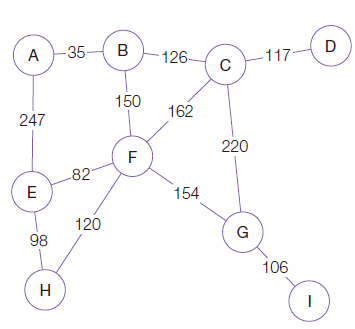
그래프의 정점 사이에 있는 모든 간선의 가중치를 오름차순으로 정렬한다.
이후 각 정점 별로 분리 집합을 만든다.
간선을 가중치 순으로 정렬하고 각 정점별로 분리 집합을 만들었다면 준비가 끝났다.
가장 작은 가중치를 가진 간선은 가중치 35인 A-B
정점 A와 B는 별개의 분리 집합 원소이므로 이 둘을 최소 신장 트리에 추가하고 간선으로 연결
분리 집합 {A}와 {B}에 대해 합집합을 수행하여 하나의 분리 집합으로 생성
두 번째로 작은 가중치를 가진 간선은 E-F(82)
E-F를 최소 신장 트리에 추가하고 분리 집합 {E}와 {F}를 합하여 하나의 분리 집합으로 생성
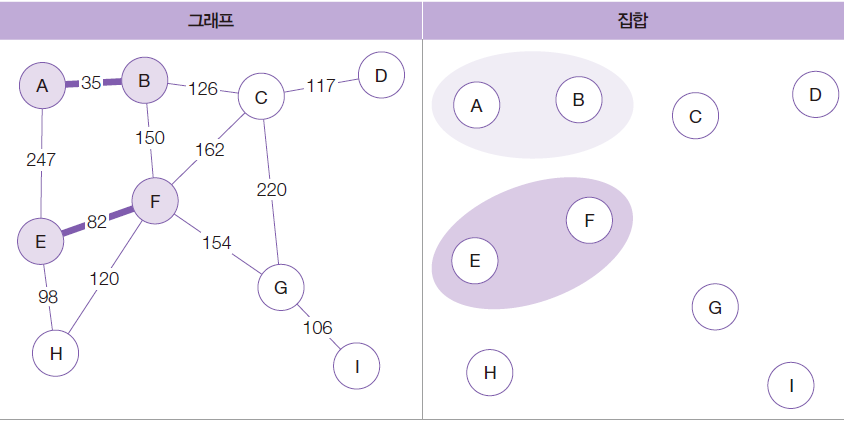
간선 E-H를 최소 신장 트리에 추가
{E, F}와 {H}에 대해 합집합을 수행
간선 G-I를 최소 신장 트리에 입력
{G}와 {I}에 대해서는 합집합 연산을 수행해서 {G, I}을 생성
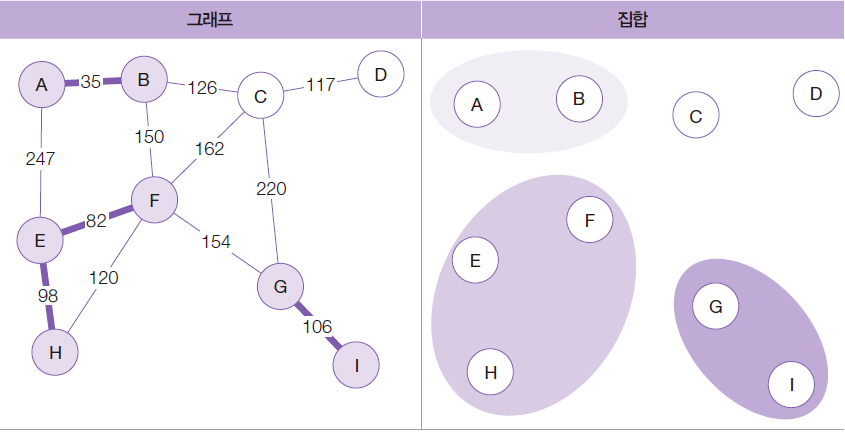
간선 F-H는 같은 집합이므로(E-F-H에 이르는 사이클이 형성되어 있으므로), 간선 F-H는 무시한다.
따라서 다음 순위의 간선을 채택 다음 순위의 간선은 가중치 117을 가진 C-D인데, 이 둘은 서로 다른 집합에 소속되어 있으므로 최소 신장 트리에 간선을 추가하고 두 정점을 하나의 집합으로 생성
B와 C는 서로 다른 집합에 속해 있으므로 이 간선을 최소 신장 트리에 추가
B가 속한 {A, B}와 C가 속한 {C, D}에 대해 합집합을 수행
B와 F는 서로 다른 집합에 속해 있으므로 간선 B-F를 최소 신장 트리에 추가
B가 소속된 {A, B, C, D}와 F가 소속된 {E, F, H}에 대해 합집합을 수행
F와 G는 서로 다른 집합에 속해 있으므로 간선 F-G를 최소 신장 트리에 추가
{A, B, C, D, E, F, H}와 {G, I}를 하나로 만들기 위해 합집합을 수행
모든 정점이 하나의 집합 안에 모여서 최소 신장 트리가 되었다.
남은 간선들은 사이클을 형성하는 것들 뿐이다.
'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [Java] 정렬 알고리즘(Sorting Algorithm) (1) | 2024.01.15 |
|---|---|
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (1) | 2023.12.19 |
| [알고리즘] 그래프 위상 정렬(Topological sorting) (1) | 2023.12.17 |
| [알고리즘]보이어-무어(Boyer-Moore) 문자열 탐색 알고리즘 (1) | 2023.11.29 |
| [Java]KMP 문자열 탐색 알고리즘 (2) | 2023.11.28 |