![[알고리즘] 그래프 위상 정렬(Topological sorting)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fr4M3a%2FbtsB17QpJRA%2FAAAAAAAAAAAAAAAAAAAAAIMpC4Km5pPLFh1MmeIcFsTqX8qolOnDvydRca4gqirV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Db5FM0Da99kTJW4MoaYifiw2Ttz0%253D)

이 글은 이것이 자료구조+알고리즘이다 with C 언어(저자:박상현) 책 내용을 개인적으로 정리하는 글임을 알립니다.
위상 정렬
- 위상 : 어떤 정점이 다른 정점과의 관계 속에서 가지는 위치
이 말은 그래프 내 서로 인접한 정점 사이의 관계에 위치라는 속성이 존재한다는 뜻이다.
이 위치는 앞/뒤일 수도 있고, 위/아래일 수도 있다.
이 글에서는 앞/뒤 관계라고 가정한다.
- 앞:간선을 뻗어내는 정점
- 뒤: 간선을 받아들이는 정점
이 앞/뒤를 차근차근 정렬하는 작업이 위상 정렬이다.
위상 정렬은 순서가 정해져 있는 작업을 차례로 수행해야 할 때, 그 순서를 결정해 주기 위해 사용한다.
위상 정렬은 여러 개의 답이 존재할 수 있다.
위상 정렬의 시간복잡도
V = 정점의 개수, E = 간선의 개수
O(V + E)
위상 정렬을 하려면 아래와 같은 조건이 있다.
- 그래프에 방향성이 있음
- 그래프 내에 사이클이 없음
이러한 그래프를 DAG(Directed Acyclic Graph)라고 한다.

위상 정렬의 동작 방식
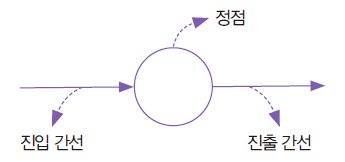
- 방향성 간선 : 두 정점이 이웃 또는 인접 관계에 있다는 사실 뿐만 아니라 어느 정점이 앞이고 어느 정점이 뒤인지도 설명
- 진입 간선(Incoming Edge) : 정점으로 들어가는 간선
- 진출 간선(Outgoing Edge) : 정점에서 나가는 간선
위상 정렬의 과정
❶ : 리스트(또는 큐)를 하나 준비
❷ : 그래프에서 진입 간선이 없는 정점을 리스트에 추가하고 해당 정점 자신과 진출 간선을 제거
❸ : 모든 정점에 대해 단계 ❷를 반복하고 그래프 내에 정점이 남아 있지 않으면 정렬을 종료, 이때 리스트에는 위상 정렬된 그래프가 저장
진입 간선이 없는 정점 A, B가 있다.
- 여기서 A와 B중 아무거나 상관없지만, B를 선택
- B를 리스트에 추가하고 B와 진출 간선을 모두 제거

B를 제거한 후 진입 간선이 없는 정점으로 A와 E가 남음
- 어느 쪽을 먼저 제거해도 상관없지만 E를 선택
- E를 리스트에 추가하고 E와 진출 간선을 제거

진입 간선이 없는 정점이 A 하나뿐이다.
- A를 리스트에 추가하고 A와 진출 간선을 모두 제거한다.

진입 간선이 없는 정점은 C, D
- 어느쪽을 먼저 제거해도 상관없지만 D를 제거
- D를 리스트에 추가하고 진출 간선을 제거

진입 간선이 없는 정점은 C,G
- 어느 쪽을 먼저 제거해도 상관 없지만 G를 제거
- G를 리스트에 추가하고 진출 간선을 제거
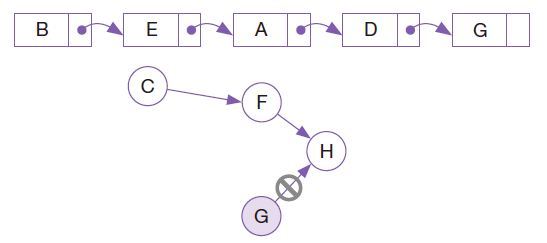
진입 간선이 없는 정점은 C
- C를 리스트에 추가하고 진출 간선을 제거

진입 간선이 없는 정점은 F
- F를 리스트에 추가하고 진출 간선을 제거

마지막으로 남은 정점 H를 리스트에 추가
- 완성된 리스트가 바로 그래프를 위상 정렬한 결과

DFS를 이용한 위상 정렬
❶ : 리스트(또는 스택)를 하나 준비
❷ : 그래프에서 진입 간선이 없는 정점에 대해 깊이 우선 탐색을 시행하고, 탐색 중에 더 이상 옮겨갈 수 있는 인접 정점이 없는 정점을 만나면 이 정점을 리스트의 새로운 ‘헤드’로 입력
❸ : ❷를 반복하다가 더 이상 방문할 정점이 없으면 깊이 우선 탐색을 종료 깊이 우선 탐색이 끝나면 리스트에 위상 정렬된 그래프가 남음
리스트를 하나 준비
진입 간선이 없는 정점을 찾아 DFS를 시작
진입 간선이 없는 정점은 A, B
어느쪽을 먼저 해도 상관없지만 A부터 탐색 시작

H에서 옮겨갈 수 있는 인접 정점이 더 이상 없으므로 H를 리스트의 ‘헤드’로 삽입
H에서 뒤로 돌아오면 정점 F를 만난다.
F의 유일한 인접 정점은 H인데, H는 이미 방문했으므로 F를 리스트의 헤드로 삽입하고 뒤로 돌아간다.
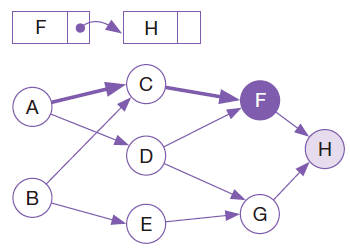
유일한 인접 정점이 F였는데, F는 이미 방문했으므로 C를 리스트의 헤드로 삽입하고 뒤로 돌아간다.

정점 A의 인접 정점은 C, D
C는 이미 방문했고, D는 아직 방문하지 않았으므로 D를 타고 DFS 수행
D를 거쳐 G에 도착하면 G의 유일한 인접 정점이었던 H가 이미 방문한 상태
따라서 G는 방문할 수 있는 인접 정점이 없는 상태이므로 이 정점을 리스트의 헤드로 삽입하고 뒤로 돌아감

유일한 인접 정점이 G였는데, G를 이미 방문했으므로 D를 리스트 헤드에 추가하고 뒤로 돌아감

다시 A로 돌아왔다.
A도 방문할 인접 정점이 없으므로 리스트의 헤드로 삽입

B를 타고 DFS 수행
B의 인접 정점 C와 E 중 C는 이미 방문한 상태이므로 E를 방문
E의 유일한 정점이었던 G는 이미 방문한 상태이므로 E를 리스트 헤드에 삽입하고 뒤로 돌아감

더 이상 방문할 수 있는 인접 정점이 없으므로 B를 리스트의 헤드로 삽입
DFS와 위상정렬이 모두 종료됨
여기서의 리스트 순서는 위상 정렬의 결과물

'자료구조 & 알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 (1) | 2023.12.19 |
|---|---|
| [알고리즘] 최소 신장 트리(Minimum Spanning Tree) (1) | 2023.12.18 |
| [알고리즘]보이어-무어(Boyer-Moore) 문자열 탐색 알고리즘 (1) | 2023.11.29 |
| [Java]KMP 문자열 탐색 알고리즘 (2) | 2023.11.28 |
| [Java] 라빈-카프 문자열 탐색 알고리즘 (2) | 2023.11.25 |
![[알고리즘] 다익스트라(Dijkstra) 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbOn2C3%2FbtsB7iQsnIl%2FAAAAAAAAAAAAAAAAAAAAAIUsBzwq1gPXP-c-2IkY-BSs69qllGFNPoK3vfLBZF98%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DNY7%252FUEjzSotudr3cEtr52n0l%252B%252FI%253D)
![[알고리즘] 최소 신장 트리(Minimum Spanning Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fd1qQoN%2FbtsB3uxF8xX%2FAAAAAAAAAAAAAAAAAAAAAC-zp5et6VPskAKFVeeCNgJTkSN_gPNX7A59uFkuNL2l%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DY4xWhWdGeTIP0vYP67hSUwatX64%253D)
![[알고리즘]보이어-무어(Boyer-Moore) 문자열 탐색 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F2G4z8%2FbtsASewkACU%2FAAAAAAAAAAAAAAAAAAAAAPHJg_E7xJz3qsTAswzHn9FEAD_0IvGpRKZBgw04_rRE%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DhbE5QmyrA1tcgTsmq8pPAbgJ410%253D)
![[Java]KMP 문자열 탐색 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FLeVuT%2FbtsATOC7INH%2FAAAAAAAAAAAAAAAAAAAAABEijg8tBNsDKLSlevDOTCh0kvXnG7XKvlNgHhjjI6bo%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DQIjPwXy6ZxWhiHrlfm2CT%252BoUHIM%253D)