

수학 관련 교양과목을 듣다가 과제로 실생활에 있는 수학에 대해 조사 해오라 해서, 얼마 전 유튜브 알고리즘이 나를 벤포드의 법칙으로 이끌어서 주제는 이걸로 정했고, 조사해 보다가 흥미로워서 적어본다.
벤포드의 법칙이란
어떠한 수치데이터에서 아라비아의 숫자 중에서 그 숫자의 앞자리만 놓고 봤을 경우
1부터 9까지 숫자 중 1이 가장 많이 사용된다는 법칙
12412, 252355, 745734, 86264 이렇게 수치 데이터가 있다고 하면, 각 앞자리는 1, 2, 7, 8이다
이렇게 여러개의 데이터를 뽑으면 1~9까지 수중에서 각 숫자가 사용될 확률이 11.11%가 아니라 1이 가장 많이 사용된다는 법칙
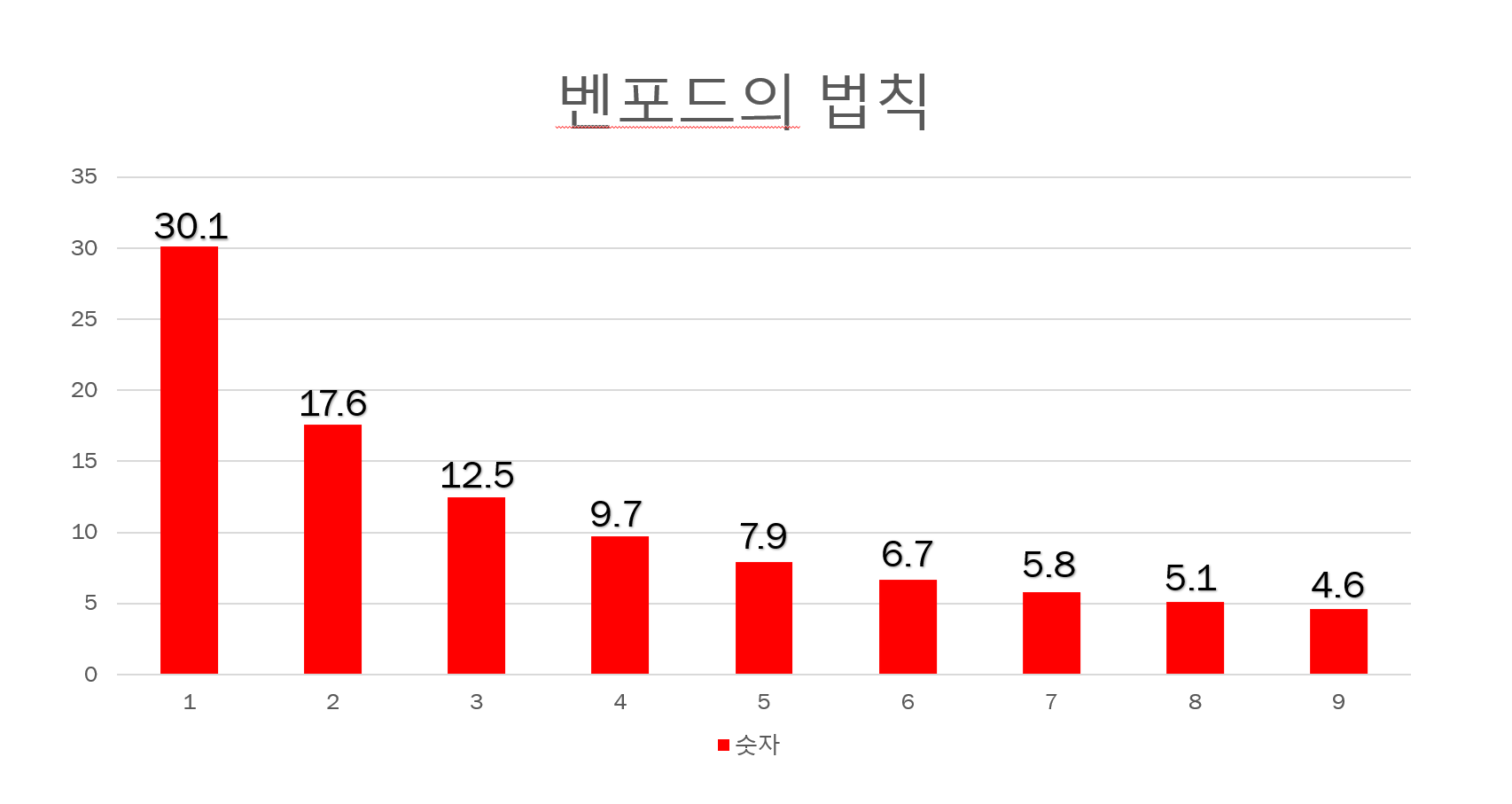
그림과 같이 1이 가장 많이 사용되고 9로 갈수록 빈도가 낮아진다.
이를 수식으로 나타내면

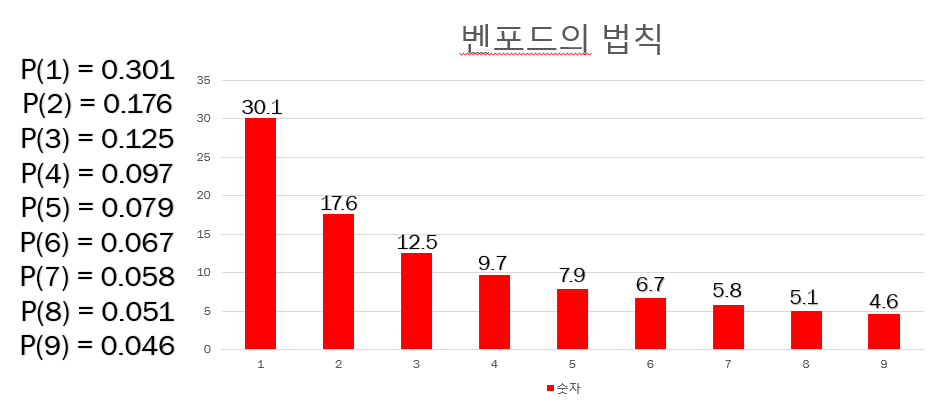
식의 결과 값과 벤포드의 법칙의 각 숫자 비율과 똑같은 것을 알 수 있다.
원리
내가 알아본 바를 예시를 들어 쉽게 설명하자면
- 보통 데이터들은 1로 시작한다. 그리하여 1로 시작하는 데이터가 가장 많을 수밖에 없고
- 1에서 2로 넘어갈 때 가장많은 시차가 발생한다.
어떤 불량식품이 천원이라고 할 때,
천원에서 이천원으로 가격 인상을 하면 100% 증가한 것이다.
2천원에서 3천 원으로 인상하는 것은 50% 증가이다.
3천원에서 4천 원으로 인상하는 것은 33.3% 증가이다.
즉, 천원에서 2천원으로 가격을 올릴 때 가장 많은 시간이 걸린다
9천원이 되었다면 11%만 인상해도 다시 앞자리 수가 1인 만원이 된다.
만원에서 2만원이 되려면 100%가 상승해야 하니 다시 시간이 오래 걸릴 수밖에 없다.
따라서 앞자리가 낮은 숫자일 수록 머무는 체류시간이 길어지고, 세상에는 앞자리 수가 1인 숫자가 많아질 수밖에 없다.
활용 분야
벤포드의 법칙은 여러 분야에서 쓰인다.
대표적으로 기업들의 회계 데이터 분석에 쓰인다.
기업들의 회계 데이터를 분석하면 벤포드의 법칙을 그대로 따르는데, 반대로 이법칙을 이용하면 회계장부를 조작한 기업을 적발할 수 있다.
예전에 대표적인 사기기업 엔론의 회계 데이터를 조사했는데

표와 같이 벤포드의 법칙을 따르지 않는 것을 볼 수 있다.
그리하여 엔론은 파산한다.
뿐만아니라 전 세계의 GDP 첫 숫자 비율과 벤포드 비율이 거의 유사하다.
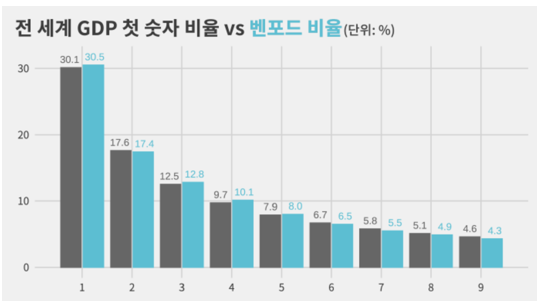
또한, 지구와 별까지의 거리, 국가별 인구수, 트위터 팔로우 수, 테러에 의한 부상자 수, 휴대폰 비밀번호 첫 앞자리 등등 여러 데이터가 벤포드의 법칙을 따른다.
벤포드의 법칙은 무적의 법칙일까?
이 법칙을 이용하면 로또 부자가 될 수 있을 거라고 생각한 사람 무조건 있을 거다.
근데 아쉽게도 로또에는 이 법칙이 성립이 안된다.
로또는 45개의 공에 편의를 위해 아라비아 숫자를 표기했을 뿐, 로또 번호는 엄밀히 숫자가 아니다.
2, 35, 26이라는 로또 공에 강아지, 메뚜기, 무당벌레라고 표기해도 로또 시스템엔 전혀 문제가 없다.
또한 수치 데이터가 아니라 그냥 랜덤인 숫자들 사이에도 이 법칙은 성립하지 않는 것으로 보인다.
아래는 파이썬을 이용해서 1~100만까지의 수중에서 만개의 수를 랜덤으로 뽑고, 수들의 앞자리만 추출하는 코드이다.
import random
numbers = []
while True:
if len(numbers) == 10000:break
RN = random.randint(1,1000000)
numbers.append(RN)
print(numbers)
i_numbers = []
for i in numbers:
if i < 10:
i_numbers.append(i)
elif i <100:
i_numbers.append(i // 10)
elif i <1000:
i_numbers.append(i // 100)
elif i < 10000:
i_numbers.append(i // 1000)
elif i < 100000:
i_numbers.append(i // 10000)
elif i < 1000000:
i_numbers.append(i // 100000)
print(i_numbers)
counter = {1 : 0, 2 : 0, 3 : 0, 4 : 0, 5 : 0, 6 : 0, 7 : 0, 8 : 0, 9 : 0}
for number in i_numbers:
counter[number] += 1
print(counter)
for i in counter:
a = counter[i] / 10000
print(a)
결과를 보면 각 숫자들이 나올 확률이 거의 11.11%에 근접하는 것을 볼 수 있다.
따라서 랜덤 성이 극도로 높거나, 정규분포를 따르는 데이터, 균일 분포를 따르는 데이터, 주사위 확률처럼 균등한 분포를 보이는 데이터 등은 벤포드의 법칙을 따르지 않는다고 볼 수 있다.
벤포드의 법칙은 만능의 법칙이 아니다.
'기타' 카테고리의 다른 글
| 카멜 케이스, 파스칼 케이스, 스네이크 케이스 (0) | 2023.07.03 |
|---|---|
| 향상된 for문 (1) | 2023.02.13 |
| 순서도(Flowchart) (0) | 2023.01.16 |
| BCD 코드와 3초과 코드 (1) | 2022.12.24 |
| 진수, 진법 변환, 보수 (0) | 2022.11.29 |



