[Java] 백준 11660번 문제(구간 합 구하기 5)

문제설명

 

 

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Boj_11660 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();
        String NM = br.readLine();
        st = new StringTokenizer(NM);
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int[][] nxn = new int[N + 1][N + 1];
        int[][] prefixSum = new int[N + 1][N + 1];

        for (int i = 1; i <= N; ++i) {
            String inputRow = br.readLine();
            st = new StringTokenizer(inputRow);
            for (int j = 1; j <= N; ++j) {
                nxn[i][j] = Integer.parseInt(st.nextToken());
                prefixSum[i][j] = nxn[i][j] + prefixSum[i - 1][j] + prefixSum[i][j - 1] - prefixSum[i - 1][j - 1];
            }
        }

        for (int i = 0; i < M; ++i) {
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());

            int result = prefixSum[x2][y2] - prefixSum[x1 - 1][y2] - prefixSum[x2][y1 - 1] + prefixSum[x1 - 1][y1 - 1];
            sb.append(result).append('\n');
        }
        System.out.print(sb);
    }
}

 

설명

• 이 문제의 핵심 개념은 누적 합이다.
• 부분합(prefix sum) 배열을 이해하려면, 이 배열이 무엇을 하는지부터 이해하는 것이 중요하다. 이 배열은 특정 구간의 합을 빠르게 계산할 수 있도록 도와준다. 이차원 배열에서는 특정 영역의 합을 효율적으로 계산하기 위해 부분합 배열을 사용한다.
• prefixSum[i][j]=nxn[i][j]+prefixSum[i−1][j]+prefixSum[i][j−1]−prefixSum[i−1][j−1]
  이 공식은 현재 위치까지의 누적 합을 계산하는 데 사용된다. 각 항목의 의미는 아래와 같다.
  nxn[i][j]: 현재 위치의 원래 배열 값
  prefixSum[i-1][j]: 현재 위치의 윗줄까지의 누적합
  prefixSum[i][j-1]: 현재 위치의 왼쪽 열까지의 누적합
  prefixSum[i-1][j-1]: 윗줄과 왼쪽 열의 겹치는 부분을 두 번 더했기 때문에 한 번 빼줌
• prefixSum[x2][y2] - prefixSum[x1 - 1][y2] - prefixSum[x2][y1 - 1] + prefixSum[x1 - 1][y1 - 1]
  이 공식의 누적 합을 이용하여 구간 합을 계산하는데 사용된다. 각 부분의 의미는 아래와 같다.
  prefixSum[x2][y2]: (1,1)부터 (x2,y2)까지의 부분 합이다.
  prefixSum[x1 - 1][y2]: (1,1)부터 (x1-1,y2)까지의 부분 합을 빼준다. 이는 x1보다 위쪽의 구간을 빼주는 역할을 한다.
  prefixSum[x2][y1 - 1]: (1,1)부터 (x2,y1-1)까지의 부분 합을 빼준다. 이는 y1보다 왼쪽의 구간을 빼주는 역할을 한다.
  prefixSum[x1 - 1][y1 - 1]: (1,1)부터 (x1-1,y1-1)까지의 부분 합을 더해준다. 이는 두 번 빼진 겹치는 구간을 다시 더해주는 역할을 한다.

 

아직 이해가 되지 않는다면, 아래의 예시를 통해 이해할 수 있다.

1. 누적 합 배열 만들기

 

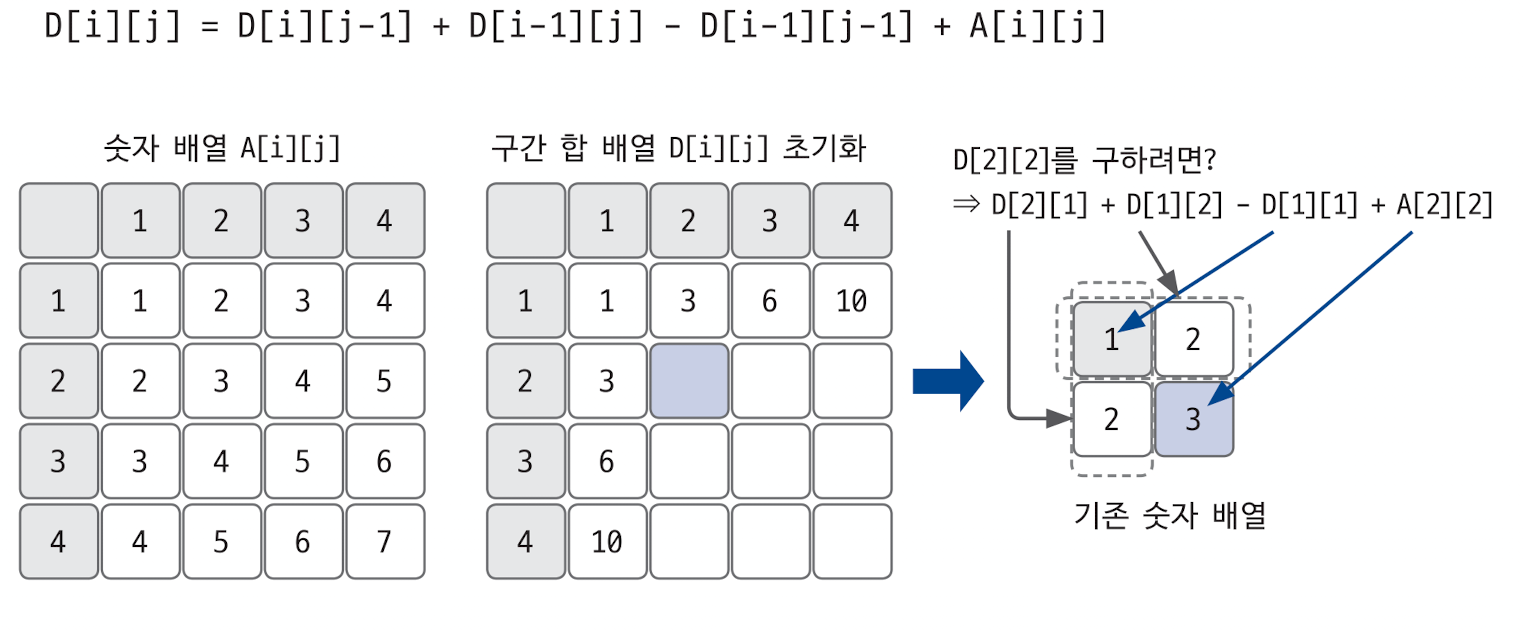
2. 누적 합 배열을 이용하여 구간 합 계산하기

예를 들어 질의가 2 2 3 4 라면

(3, 4) 구간 합에서 (1, 4) 구간합, (3, 1) 구간 합을 뺀 다음 중복하여 뺀(1, 1) 구간합을 더하면 된다.

 

그림 출처 : Do It! 알고리즘 코딩 테스트 - 자바편